题目内容
设某大学的女生体重 (单位:
(单位: )与身高
)与身高 (单位:
(单位: )具有线性相关关系,根据一组样本数据
)具有线性相关关系,根据一组样本数据 ,用最小二乘法建立的回归方程为
,用最小二乘法建立的回归方程为 ,则下列结论中不正确的是( )
,则下列结论中不正确的是( )
A. 与 与 具有正的线性相关关系 具有正的线性相关关系 |
B.回归直线过样本点的中心 |
| C.若该大学某女生身高增加lcm,则其体重约增加0.85kg |
| D.若该大学某女生身高为170cm,则可断定其体重必为58.79kg |
D.
解析试题分析:根据回归方程为 知,
知, ,所以
,所以 与
与 具有正的线性相关关系,故
具有正的线性相关关系,故 正确;又因为回归直线过样本点的中心
正确;又因为回归直线过样本点的中心 ,故
,故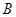 正确;因为
正确;因为 ,所以该大学某女生身高增加lcm,则其体重约增加0.85kg,故
,所以该大学某女生身高增加lcm,则其体重约增加0.85kg,故 正确;当
正确;当 时,
时, ,但这是预测值,不可断定其体重为58.79kg,故
,但这是预测值,不可断定其体重为58.79kg,故 不正确.
不正确.
考点:回归分析的初步应用.

练习册系列答案
相关题目
某小卖部销售一品牌饮料的零售价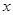 (元/评)与销售量
(元/评)与销售量 (瓶)的关系统计如下:
(瓶)的关系统计如下:
| 零售价x(元/瓶) | 3.0 | 3.2 | 3.4 | 3.6 | 3.8 | 4.0 |
| 销量y(瓶) | 50 | 44 | 43 | 40 | 35 | 28 |
已知的关系符合线性回归方程
 ,其中
,其中 .当单价为4.2元时,估计该小卖部销售这种品牌饮料的销量为( )
.当单价为4.2元时,估计该小卖部销售这种品牌饮料的销量为( )A.20 B.22 C.24 D.26
下表提供了某厂节能降耗技术改造后生产某产品过程中记录的产量 (吨)与相应的生产能耗
(吨)与相应的生产能耗 (吨)的几组对应数据. 根据表中提供的数据,求出
(吨)的几组对应数据. 根据表中提供的数据,求出 关于
关于 的线性回归方程是
的线性回归方程是 ,那么表中
,那么表中 的值是( )
的值是( )
 | 3 | 4 | 5 | 6 |
 | 2.5 |  | 4 | 4.5 |
A.
 B.
B. C.
C. D.
D.
下表是某厂1—4月份用水量(单位:百吨)的一组数据:
| 月份x | 1 | 2 | 3 | 4 |
| 用水量y | 4.5 | 4 | 3 | 2.5 |
由散点图可知,用水量与月份之间有较好的线性相关关系,其线性回归方程为
 =-0.7x+a,则a等于( )
=-0.7x+a,则a等于( )A.10.5 B.5.15 C.5.2 D.5.25
若对于预报变量y与解释变量x的10组统计数据的回归模型中,计算R2=0.95,又知残差平方和为120.55,那么 的值为( )
的值为( )
| A.241.1 | B.245.1 | C.2411 | D.2451 |






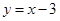


 设其平均数为
设其平均数为 ,中位数为
,中位数为 ,众数为
,众数为 ,则有( )
,则有( ) B.
B. C.
C. D.
D.