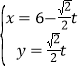题目内容
【题目】进入12月以来，某地区为了防止出现重污染天气，坚持保民生、保蓝天，严格落实机动车限行等一系列“管控令”，该地区交通管理部门为了了解市民对“单双号限行”的赞同情况，随机采访了220名市民，将他们的意见和是否拥有私家车情况进行了统计，得到如下的2×2列联表：
| 赞同限行 | 不赞同限行 | 合计 |
没有私家车 | 90 | 20 | 110 |
有私家车 | 70 | 40 | 110 |
合计 | 160 | 60 | 220 |
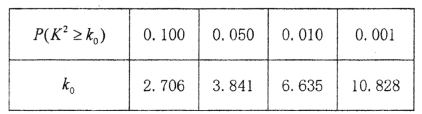
（1）根据上面的列联表判断，能否有99%的把握认为“赞同限行与是否拥有私家车”有关；
（2）为了解限行之后是否对交通拥堵、环境污染起到改善作用，从上述调查的不赞同限行的人员中按分层抽样抽取6人，再从这6人中随机抽出2名进行电话回访，求抽到的2人中至少有1名“没有私家车”人员的概率．
参考公式：K2＝
P（K2≥k） | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
k | 2.706 | 3..841 | 6.635 | 7.879 | 10.828 |
【答案】（1）有
的把握认为“赞同限行与是否拥有私家车有关”；（2）
【解析】
（1）根据列联表里的数据，计算出
的值，然后进行判断；（2）根据分层抽样的要求得到没有私家车的应抽取2人 有私家车的4人，再求出总的情况数和符合要求的情况数，由古典概型公式，得到答案.
解：（1）根据列联表,计算
所以有
的把握认为“赞同限行与是否拥有私家车有关”；
（2）从不赞同限行的人员中按分层抽样法抽取6人，
没有私家车的应抽取2人 有私家车的4人.
随机抽出2人，总的情况数为
，
至少有1名“没有私家车”人员的情况数为
，
所以根据古典概型的公式得：
．
阅读快车系列答案
【题目】某同学用“五点法”画函数
在某一个周期内的图象时，列表并填入了部分数据，如下表：
| 0 |
| π |
| 2π |
x |
|
| |||
| 0 | 4 | -4 | 0 |
（1）请将上表数据补充完整，填写在答题卡上相应位置，并直接写出函数f（x）的解析式；
（2）将
图象上所有点向左平行移动θ（
）个单位长度，得到
的图象.若图象的一个对称中心为
，求θ的最小值.
【题目】在中学生综合素质评价某个维度的测评中，分优秀、合格、尚待改进三个等级进行学生互评.某校高一年级有男生500人，女生400人，为了了解性别对该维度测评结果的影响，采用分层抽样方法从高一年级抽取了45名学生的测评结果，并作出频数统计表如下：
表一：男生
男生 | 等级 | 优秀 | 合格 | 尚待改进 |
频数 | 15 |
| 5 |
表二：女生
女生 | 等级 | 优秀 | 合格 | 尚待改进 |
频数 | 15 | 3 |
|
（1）求
,
的值；
（2）从表二的非优秀学生中随机抽取2人交谈，求所选2人中恰有1人测评等级为合格的概率；
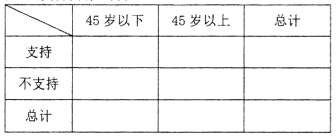
（3）由表中统计数据填写
列联表，并判断是否有90%的把握认为“测评结果优秀与性别有关”.
男生 | 女生 | 总计 | |
优秀 | |||
非优秀 | |||
总计 | 45 |
参考公式：
，其中
.
参考数据：
| 0.01 | 0.05 | 0.01 |
| 2.706 | 3.841 | 6.635 |
【题目】如表提供了工厂技术改造后某种型号设备的使用年限
和所支出的维修费
（万元）的几组对照数据：
| 2 | 3 | 4 | 5 | 6 |
| 1 | 2.5 | 3 | 4 | 4.5 |
参考公式：
，
.
（1）若知道对呈线性相关关系，请根据上表提供的数据，用最小二乘法求出关于的线性回归方程
；
（2）已知该工厂技术改造前该型号设备使用10年的维修费用为9万元，试根据（1）求出的线性回归方程，预测该型号设备技术改造后，使用10年的维修费用能否比技术改造前降低？
