题目内容
等差数列{an}的前n项和为Sn ,已知S10=0,S15 =25,则nSn 的最小值为________.
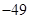
由题意知: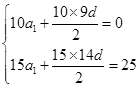 ,解得
,解得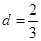 ,
,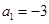 ,所以
,所以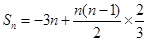
=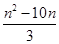 ,即nSn =
,即nSn =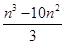 ,令
,令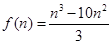 ,则有
,则有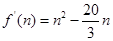 ,令
,令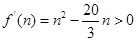 得,
得,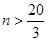 ,令
,令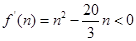 得,
得,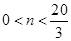 ,又因为n为正整数,所以当
,又因为n为正整数,所以当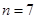 时,
时,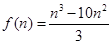 所以取得最小值,即nSn 的最小值为
所以取得最小值,即nSn 的最小值为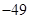 .
.
【考点定位】本小题主要考查等差数列的前n项和公式的应用、导数求数列这一特殊函数的最值,要注意n取正整数这一条件,考查同学们分析问题、解决问题的能力.
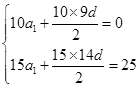 ,解得
,解得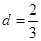 ,
,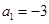 ,所以
,所以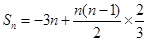
=
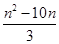 ,即nSn =
,即nSn =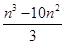 ,令
,令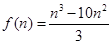 ,则有
,则有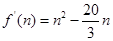 ,令
,令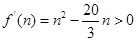 得,
得,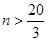 ,令
,令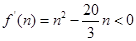 得,
得,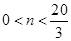 ,又因为n为正整数,所以当
,又因为n为正整数,所以当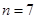 时,
时,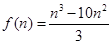 所以取得最小值,即nSn 的最小值为
所以取得最小值,即nSn 的最小值为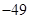 .
.【考点定位】本小题主要考查等差数列的前n项和公式的应用、导数求数列这一特殊函数的最值,要注意n取正整数这一条件,考查同学们分析问题、解决问题的能力.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
 的等比数列
的等比数列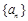 的前n项和为
的前n项和为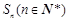 , 且
, 且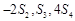 成等差数列.
成等差数列. 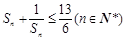 .
. 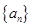 中,已知
中,已知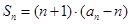 (
(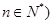 .
.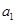 及
及 ;
;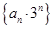 的前
的前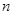 项和
项和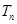 .
.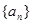 的前n项和为
的前n项和为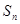 , 公差为d, 已知
, 公差为d, 已知
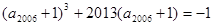 , 则下列结论正确的是 ( )
, 则下列结论正确的是 ( )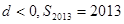
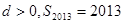
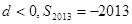
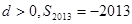
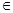 N+)的前n项和,且a1=3,a4=9,则S5=
N+)的前n项和,且a1=3,a4=9,则S5= 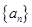 中,已知
中,已知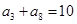 ,则
,则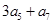
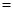 _____.
_____. ,如果存在实常数
,如果存在实常数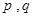 使得
使得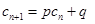 对于任意
对于任意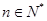 都成立,我们称数列
都成立,我们称数列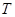 数列”.
数列”.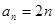 ,
,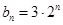 ,
,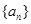 、
、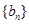 是否为“
是否为“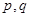 ,若不是,请说明理由;
,若不是,请说明理由;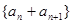 也是“
也是“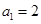 ,
,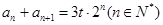 ,
,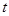 为常数.求数列
为常数.求数列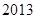 项的和.
项的和. 中,
中, 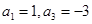
 项和
项和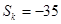 ,求
,求