题目内容
A、B是单位圆O上的动点,且A、B分别在第一、二象限.C是圆O与x轴正半轴的交点,△AOB为正三角形.记∠AOC=α.
(1)若A点的坐标为 ,求
,求 的值;
的值;
(2)求 的取值范围.
的取值范围.
(1)若A点的坐标为
 ,求
,求 的值;
的值;(2)求
 的取值范围.
的取值范围.(1) 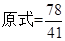
(2) |BC|2的取值范围是(2,2+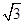 ).
).
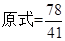
(2) |BC|2的取值范围是(2,2+
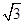 ).
).试题分析:(1)∵A点的坐标为
 ,
,∴tanα=
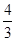 ,
,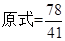
(2)设A点的坐标为(cosα,sinα),
∵△AOB为正三角形,
∴B点的坐标为(cos(α+
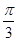 ),sin(α+
),sin(α+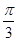 )),且C(1,0),
)),且C(1,0),∴|BC|2=[cos(α+
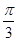 )-1]2+sin2(α+
)-1]2+sin2(α+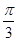 )
)=2-2cos(α+
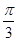 ).
).而A、B分别在第一、二象限,
∴α∈(
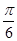 ,
,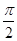 ).
).∴α+
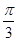 ∈(
∈(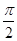 ,
,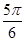 ),
),∴cos(α+
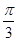 )∈(-
)∈(-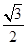 ,0).
,0).∴|BC|2的取值范围是(2,2+
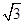 ).
).点评:解决的关键是利用三角函数的公式以及三角函数的性质熟练的表示,属于基础题。

练习册系列答案
相关题目
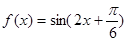 ,下列命题:
,下列命题: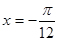 对称; ②函数图象关于点
对称; ②函数图象关于点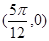 对称;
对称;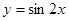 的图象向左平移个
的图象向左平移个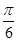 单位而得到;
单位而得到;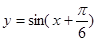 的图象上所有点的横坐标缩短到原来的
的图象上所有点的横坐标缩短到原来的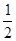 倍(纵坐标不变)而得到;其中正确命题的序号是 .
倍(纵坐标不变)而得到;其中正确命题的序号是 . 的值为________________.
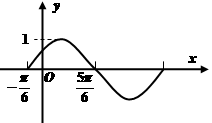
的值为________________.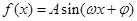 的图像如图所示,其中
的图像如图所示,其中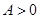 ,
,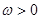 ,
,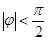 .
.
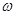 、
、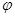 的值;
的值;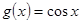 经过平移变换可否得到函数
经过平移变换可否得到函数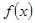 的图像?若能,平移的最短距离是多少个单位?否则,说明理由.
的图像?若能,平移的最短距离是多少个单位?否则,说明理由. ,且
,且 则
则 的取值范围是
的取值范围是  ( )
( )



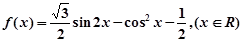
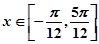 时,求函数
时,求函数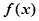 的最小值和最大值;
的最小值和最大值;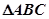 的内角
的内角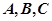 的对应边分别为
的对应边分别为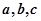 ,且
,且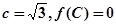 ,若向量
,若向量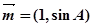 与向量
与向量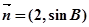 共线,求
共线,求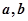 的值.
的值.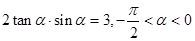 ,则
,则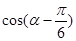 的值是 .
的值是 . 的值;
的值;