Question

【题目】如图，已知三棱锥P－ABC中，PA平面ABC，ABAC，且PA＝l，AB＝AC＝2，点D满足，.

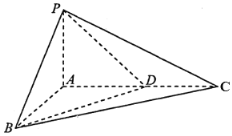
（1）当，求二面角P－BD－C的余弦值；

（2）若直线PC与平面PBD所成角的正弦值为，求的值.

Answer 1

【答案】（1）（2）

【解析】

（1）由题意，以为正交基底，建立空间直角坐标系A—xyz，求出各点的坐标，进而求出平面的法向量，然后利用空间向量求解二面角的大小；

（2）利用线面角的向量求法可得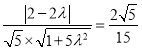，解出即可．

解：（1）∵PA⊥平面ABC，

∴AP⊥AB，AP⊥AC，

又AB⊥AC，

∴以为正交基底，建立如图所示空间直角坐标系A—xyz，

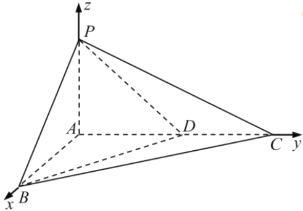
∵PA＝1，AB＝AC＝2，

∴A(0，0，0)，B(2，0，0)，C(0，2，0)，P(0，0，1)

∴，即D，

∴，，

设平面PBD的法向量为，

则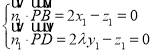，取，

当时，，又可取为平面BDC的一个法向量，

∴，

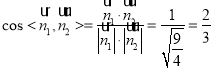由图可知二面角P—BD—C的余弦值为；

（2），平面PBD的一个法向量为，

设直线PC与平面PBD所成角为，

则，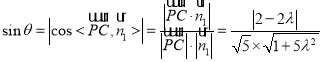

结合题设，得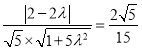，即，

解得或，

∵，

∴．