题目内容
【题目】有7个球,其中红色球2个(同色不加区分),白色,黄色,蓝色,紫色,灰色球各1个,将它们排成一行,要求最左边不排白色,2个红色排一起,黄色和红色不相邻,则有________种不同的排法(用数字回答).
【答案】408
【解析】
先不考虑白色球的限制条件,将白色,蓝色,紫色,灰色球排列起来,然后将两个红色球捆绑成一个整体与黄球插入前4个颜色的球制造出的5个空隙中,利用分步计数乘法原理可得所有的排法,再减去最左边排白色球的排法,即可得解.
不考虑白色球排列限制,先不排黄色球和红色球,其他球任意排列共有![]() 种排法,再将2个红色球(排一起)和黄色球插入5个空隙中,有
种排法,再将2个红色球(排一起)和黄色球插入5个空隙中,有![]() 种排法,即此时排法共有
种排法,即此时排法共有![]() 种,而最左边排白色球的排法共有
种,而最左边排白色球的排法共有![]() 种,故符合条件的排法共有
种,故符合条件的排法共有![]() 种.
种.
故答案为:408.

练习册系列答案
相关题目
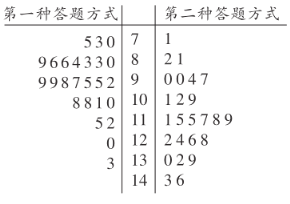
【题目】某市实验中学数学教研组,在高三理科一班进行了一次“采用两种不同方式进行答卷”的考试实验,第一种做卷方式:按从前往后的顺序依次做;第二种做卷方式:先做简单题,再做难题.为了比较这两种做卷方式的效率,选取了![]() 名学生,将他们随机分成两组,每组
名学生,将他们随机分成两组,每组![]() 人.第一组学生用第一种方式,第二组学生用第二种方式,根据学生的考试分数(单位:分)绘制了茎叶图如图所示.
人.第一组学生用第一种方式,第二组学生用第二种方式,根据学生的考试分数(单位:分)绘制了茎叶图如图所示.
![]() 若
若![]() 分(含
分(含![]() 分)以上为优秀,根据茎叶图估计两种做卷方式的优秀率;
分)以上为优秀,根据茎叶图估计两种做卷方式的优秀率;
![]() 设
设![]() 名学生考试分数的中位数为
名学生考试分数的中位数为![]() ,根据茎叶图填写下面的
,根据茎叶图填写下面的![]() 列联表:
列联表:
超过中位数 | 不超过中位数 | 合计 | |
第一种做卷方式 | |||
第一种做卷方式 | |||
合计 |
根据列联表,能否有![]() 的把握认为两种做卷方式的效率有差异?
的把握认为两种做卷方式的效率有差异?
附: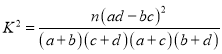 ,
,![]() .
.
|
|
|
|
|
|
|
|