题目内容
已知函数
(1)当a=2时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(2)求函数 的极值.
的极值.

(1)当a=2时,求曲线
 在点
在点 处的切线方程;
处的切线方程;(2)求函数
 的极值.
的极值.(1) ; (2)
; (2)  时,函数
时,函数 无极值;
无极值; 时,函数
时,函数 在
在 处取得极小值
处取得极小值 ,无极大值.
,无极大值.
 ; (2)
; (2)  时,函数
时,函数 无极值;
无极值; 时,函数
时,函数 在
在 处取得极小值
处取得极小值 ,无极大值.
,无极大值.试题分析:(1) 由a=2得
 的解析式,进而可求出导数
的解析式,进而可求出导数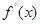 ;由导数的几何意义可知:曲线
;由导数的几何意义可知:曲线 在点
在点 处的切线的斜率
处的切线的斜率 ,从而用直线的点斜式可写出切线方程;(2)由
,从而用直线的点斜式可写出切线方程;(2)由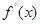 发现:当
发现:当 时
时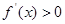 方程
方程 无解,当
无解,当 时,由
时,由 ,解得
,解得 ,因此需按
,因此需按 和
和 分类讨论.
分类讨论.试题解析:函数
 的定义域为
的定义域为 ,
, .
.当a=2时,
 ,
, ,
, 曲线
曲线 在点
在点 处的切线方程为:
处的切线方程为: ,即
,即 .
.由
 可知:
可知:①当
 时,
时, 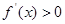 ,函数
,函数 为
为 上增函数,函数
上增函数,函数 无极值;
无极值;②当
 时,由
时,由 ,解得
,解得 ;
; 时
时 ,
, 时,
时, 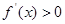
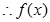 在
在 处取得极小值,且极小值为
处取得极小值,且极小值为 ,无极大值.
,无极大值.综上:当
 时,函数
时,函数 无极值;
无极值;当
 时,函数
时,函数 在
在 处取得极小值
处取得极小值 ,无极大值.
,无极大值.
练习册系列答案
相关题目
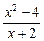 ,
,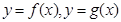 的导函数的图像如下图,那么
的导函数的图像如下图,那么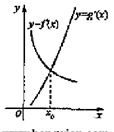

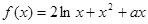 ,若曲线
,若曲线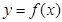 存在与直线
存在与直线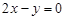 平行的切线,则实数
平行的切线,则实数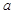 的取值范围是( )
的取值范围是( )



 在点
在点 处的切线的方程为___________
处的切线的方程为___________ 在点(1,-
在点(1,- )处切线的倾斜角为( )
)处切线的倾斜角为( )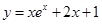 在点
在点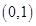 处的切线方程为 .
处的切线方程为 . 在
在 处的切线的斜率为 .
处的切线的斜率为 .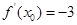 ,则
,则 ( )
( )


