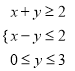题目内容
【题目】（Ⅰ）抛物线的顶点在原点，坐标轴为对称轴，并经过点
，求此抛物线的方程.
（Ⅱ）已知圆： 
（
），把圆上的各点纵坐标不变，横坐标伸长到原来的
倍得一椭圆.求椭圆方程，并证明椭圆离心率是与
无关的常数.
【答案】（1）
或
（2）
【解析】试题分析：（1）根据题意设出抛物线的标准方程，注意两种形式，把点坐标代入即可；（2）利用图像的伸缩变换得到椭圆方程，计算椭圆离心率是一常数，故与c无关．
试题解析：（Ⅰ）依题意，若焦点在
轴，设抛物线的方程为
（
）
将
代入， 
，得
，此时方程为： 
若焦点在
轴，设抛物线的方程为
（
）
将
代入， 
，得
，此时方程为： 
所以，所求抛物线的方程为
或
（Ⅱ）设
是圆： 
上任一点，则
为所求椭圆上经过变换后的对应点，
则有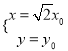
，即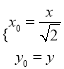
代入圆的方程得： 
．
故所求的椭圆方程为： 
．
又椭圆的长半轴的长为
，半焦距为
，故离心率
与
无关．
练习册系列答案
相关题目
【题目】国家为了鼓励节约用水，实行阶梯用水收费制度，价格参照表如表：
用水量（吨） | 单价（元/吨） | 注 |
0～20（含） | 2.5 | |
20～35（含） | 3 | 超过20吨不超过35吨的部分按3元/吨收费 |
35以上 | 4 | 超过35吨的部分按4元/吨收费 |
（1）若小明家10月份用水量为30吨，则应缴多少水费？
（2）若小明家10月份缴水费99元，则小明家10月份用水多少吨？
（3）写出水费y与用水量x之间的函数关系式，并画出函数的图象．
