题目内容
如图所示,四棱锥P ABCD的底面为正方形,侧棱PA⊥底面ABCD,且PA=AD=2,E,F,H分别是线段PA,PD,AB的中点.
ABCD的底面为正方形,侧棱PA⊥底面ABCD,且PA=AD=2,E,F,H分别是线段PA,PD,AB的中点.
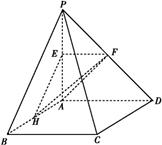
(1)求证:PB∥平面EFH;
(2)求证:PD⊥平面AHF.
 ABCD的底面为正方形,侧棱PA⊥底面ABCD,且PA=AD=2,E,F,H分别是线段PA,PD,AB的中点.
ABCD的底面为正方形,侧棱PA⊥底面ABCD,且PA=AD=2,E,F,H分别是线段PA,PD,AB的中点.
(1)求证:PB∥平面EFH;
(2)求证:PD⊥平面AHF.
(1)见解析 (2)见解析
证明:(1)∵E、H分别是PA、AB的中点,
∴EH∥PB.
又EH?平面EFH,PB?平面EFH,
∴PB∥平面EFH.
(2)∵PA⊥平面ABCD,
∴PA⊥AB.
又∵AB⊥AD,PA∩AD=A,
∴AB⊥底面PAD.
又∵PD?平面PAD,
∴AB⊥PD.
Rt△PAD中,PA=AD=2,F为PD的中点,
∴AF⊥PD.
又∵AF∩AB=A,AF?平面AHF,AB?平面AHF,
∴PD⊥平面AHF.

练习册系列答案
相关题目
 的底面
的底面 为正方形,
为正方形,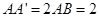 ,
,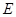 为棱
为棱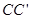 的中点.
的中点.
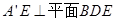 ;
;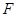 为
为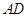 中点,
中点,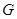 为棱
为棱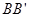 上一点,且
上一点,且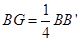 ,求证:
,求证: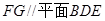 .
.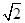 ,CE=EF=1.
,CE=EF=1.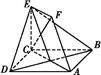
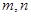 是不重合的直线,
是不重合的直线, 是不重合的平面,有下列命题:
是不重合的平面,有下列命题: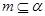 ,
,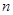 ∥
∥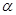 ,则
,则 ∥
∥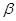 ,则
,则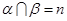 ,
,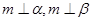 ,则
,则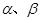 ,且
,且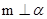 ,
,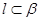 .给出下列命题:
.给出下列命题: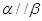 ,则
,则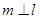 ;
;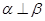 ,则
,则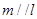 ;
;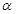 ,下列命题正确的是( )
,下列命题正确的是( ) 则
则
 则
则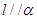
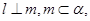 则
则
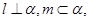 则
则