Question

【题目】设函数,已知它们在处的切线互相平行.

(1)求的值；

(2)若函数,且方程有且仅有四个解，求实数的取值范围.

Answer 1

【答案】（1）；（2）.

【解析】试题分析： 由和在处的切线互相平行可以得到，解方程即可求得的值；

分别求出和的极值，结合单调性画出的图象，结合图象可得若方程有四个解，则，解不等式求得实数的取值范围

解析：函数g(x)＝bx2－ln x的定义域为(0，＋∞)，

(1)f′(x)＝3ax2－3af′(1)＝0，

g′(x)＝2bx－g′(1)＝2b－1，

依题意得2b－1＝0，所以b＝.

(2)x∈(0，1)时，g′(x)＝x－＜0，

即g(x)在(0，1)上单调递减，

x∈(1，＋∞)时，g′(x)＝x－＞0，即g(x)在(1，＋∞)上单调递增，所以当x＝1时，g(x)取得极小值g(1)＝；

当a＝0时，方程F(x)＝a2不可能有四个解；

当a＜0，x∈(－∞，－1)时，f′(x)＜0，即f(x)在(－∞，－1)上单调递减，x∈(－1，0)时，f′(x)＞0，

即f(x)在(－1，0)上单调递增，

所以当x＝－1时，f(x)取得极小值f(－1)＝2a，

又f(0)＝0，所以F(x)的图象如图(1)所示，从图象可以看出F(x)＝a2不可能有四个解.

当a＞0，x∈(－∞，－1)时，f′(x)＞0，

即f(x)在(－∞，－1)上单调递增，

x∈(－1，0)时，f′(x)＜0，

即f(x)在(－1，0)上单调递减，

所以当x＝－1时，f(x)取得极大值f(－1)＝2a.

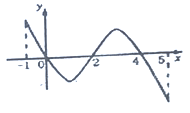
又f(0)＝0，所以F(x)的图象如图(2)所求，

从图(2)看出，若方程F(x)＝a2有四个解，则＜a2＜2a，

得＜a＜2，

所以，实数a的取值范围是.