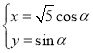ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΕ§ΦΨ÷γ“ΙΈ¬≤ν¥σ–Γ”κΡ≥Ζ¥ΦΨΫΎ¥σΕΙ–¬ΤΖ÷÷ΖΔ―ΩΕύ…Ό÷°Φδ”–ΙΊœΒΘ§Ρ≥≈©ΩΤΥυΕ‘¥ΥΙΊœΒΫχ––ΝΥΒς≤ιΖ÷ΈωΘ§ΥϊΟ«Ζ÷±πΦ«¬ΦΝΥ12‘¬1»’÷Ν12‘¬5»’ΒΡΟΩΧλ÷γ“ΙΈ¬≤ν”κ Β―ι “ΟΩΧλΟΩ100Ω≈÷÷Ή”÷–ΒΡΖΔ―Ω ΐΘ§ΒΟΒΫ»γœ¬Ή ΝœΘΚ
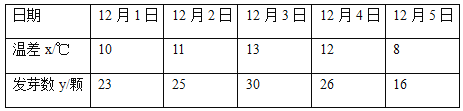
ΗΟ≈©ΩΤΥυ»ΖΕ®ΒΡ―–ΨΩΖΫΑΗ «ΘΚœ»¥”’βΈεΉι ΐΨί÷–―Γ»Γ2ΉιΘ§”Ο Θœ¬ΒΡ3Ήι ΐΨί«σœΏ–‘ΜΊΙιΖΫ≥ΧΘ§‘ΌΕ‘±Μ―Γ»ΓΒΡ2Ήι ΐΨίΫχ––Φλ―ιΘ°
Θ®1Θ©«σ―Γ»ΓΒΡ2Ήι ΐΨί«ΓΚΟ «œύΝΎ2Χλ ΐΨίΒΡΗ≈¬ ΘΜ
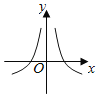
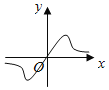
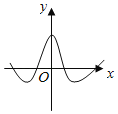
Θ®2Θ©»τ―Γ»ΓΒΡ «12‘¬1»’”κ12‘¬5»’ΒΡΝΫΉι ΐΨίΘ§«κΗυΨί12‘¬2»’÷Ν12‘¬4»’ΒΡ ΐΨίΘ§«σ≥ωyΙΊ”ΎxΒΡœΏ–‘ΜΊΙιΖΫ≥Χ![]() ΘΜ
ΘΜ
Θ®3Θ©»τ”…œΏ–‘ΜΊΙιΖΫ≥ΧΒΟΒΫΒΡΙάΦΤ ΐΨί”κΥυ―Γ≥ωΒΡΦλ―ι ΐΨίΒΡΈσ≤ν≤Μ≥§Ιΐ2Ω≈Θ§‘ρ»œΈΣΒΟΒΫΒΡœΏ–‘ΜΊΙιΖΫ≥Χ «Ω…ΩΩΒΡΘ§ ‘Έ Θ®2Θ©÷–ΥυΒΟΒΡœΏ–‘ΜΊΙιΖΫ≥Χ «ΖώΩ…ΩΩΘΩ
Θ®≤ΈΩΦΙΪ ΫΘΚ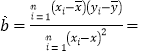 Θ§
Θ§![]() Θ°Θ©
Θ°Θ©
ΓΨ¥πΑΗΓΩ(1)![]() (2)
(2) ![]() Θ®3Θ©Θ®2Θ©÷–ΥυΒΟΒΡœΏ–‘ΜΊΙιΖΫ≥ΧΩ…ΩΩ
Θ®3Θ©Θ®2Θ©÷–ΥυΒΟΒΡœΏ–‘ΜΊΙιΖΫ≥ΧΩ…ΩΩ
ΓΨΫβΈωΓΩΖ÷ΈωΘΚΒΎ“ΜΈ ”ΟΝ–ΨΌΖ®«σΜυ±Ψ ¬Φΰ ΐΘ§ΦΤΥψΥυ«σΒΡΗ≈¬ ÷ΒΘΜΒΎΕΰΈ ”… ΐΨίΦΤΥψ![]() Θ§«σ≥ωΜΊΙι÷±œΏΖΫ≥ΧΒΡœΒ ΐΘ§–¥≥ωΜΊΙι÷±œΏΖΫ≥ΧΘΜΒΎ»ΐΈ ΦΤΥψ
Θ§«σ≥ωΜΊΙι÷±œΏΖΫ≥ΧΒΡœΒ ΐΘ§–¥≥ωΜΊΙι÷±œΏΖΫ≥ΧΘΜΒΎ»ΐΈ ΦΤΥψ![]() ±
±![]() ΒΡ÷ΒΚΆ
ΒΡ÷ΒΚΆ![]() ±
±![]() ΒΡ÷ΒΘ§‘Ό±»ΫœΒΟ≥ωΫα¬έ.
ΒΡ÷ΒΘ§‘Ό±»ΫœΒΟ≥ωΫα¬έ.
œξΫβΘΚΘ®1Θ©…η≥ιΒΫ≤ΜœύΝΎΒΡΝΫΉι ΐΨίΈΣ ¬ΦΰAΘ§¥”5Ήι ΐΨί÷–―Γ»Γ2Ήι ΐΨίΙ≤”–10÷÷«ιΩωΘΚ
Θ®1Θ§2Θ©Θ§Θ®1Θ§3Θ©Θ§Θ®1Θ§4Θ©Θ§Θ®1Θ§5Θ©Θ§Θ®2Θ§3Θ©Θ§Θ®2Θ§4Θ©Θ§Θ®2Θ§5Θ©Θ§Θ®3Θ§4Θ©Θ§Θ®3Θ§5Θ©Θ§Θ®4Θ§5Θ©Θ§
Τδ÷– ΐΨίΈΣ12‘¬ΖίΒΡ»’ΤΎ ΐΘ§ΟΩ÷÷«ιΩωΕΦ «Ω…Ρή≥ωœ÷ΒΡΘ§ ¬ΦΰAΑϋά®ΒΡΜυ±Ψ ¬Φΰ”–6÷÷ΘΜ
ΓύPΘ®AΘ©=![]() =
=![]()
![]() ΘΜΓύ―Γ»ΓΒΡ2Ήι ΐΨί«ΓΚΟ «≤ΜœύΝΎ2Χλ ΐΨίΒΡΗ≈¬ «
ΘΜΓύ―Γ»ΓΒΡ2Ήι ΐΨί«ΓΚΟ «≤ΜœύΝΎ2Χλ ΐΨίΒΡΗ≈¬ «![]()
![]() ΘΜ
ΘΜ
Θ®2Θ©”… ΐΨίΘ§«σΒΟ![]()
![]() =
=![]() ΓΝΘ®11+13+12Θ©=12Θ§
ΓΝΘ®11+13+12Θ©=12Θ§![]()
![]() =
=![]() ΓΝΘ®25+30+26Θ©=27Θ§
ΓΝΘ®25+30+26Θ©=27Θ§
”…ΙΪ ΫΘ§«σΒΟ![]()
![]() =
=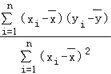 =
=![]() =2.5Θ§
=2.5Θ§
![]()
![]() =
=![]()
![]() ©¹
©¹![]()
![]()
![]()
![]() =27©¹2.5ΓΝ12=©¹3Θ§ΓύyΙΊ”ΎxΒΡœΏ–‘ΜΊΙιΖΫ≥ΧΈΣ
=27©¹2.5ΓΝ12=©¹3Θ§ΓύyΙΊ”ΎxΒΡœΏ–‘ΜΊΙιΖΫ≥ΧΈΣ![]()
![]() =2.5x©¹3ΘΜ.
=2.5x©¹3ΘΜ.
Θ®3Θ©Β±x=10 ±Θ§![]()
![]() =2.5ΓΝ10©¹3=22Θ§|22©¹23|ΘΦ2ΘΜ
=2.5ΓΝ10©¹3=22Θ§|22©¹23|ΘΦ2ΘΜ
Ά§―υΒ±x=8 ±Θ§![]()
![]() =2.5ΓΝ8©¹3=17Θ§|17©¹16|ΘΦ2ΘΜ
=2.5ΓΝ8©¹3=17Θ§|17©¹16|ΘΦ2ΘΜ
ΓύΘ®2Θ©÷–ΥυΒΟΒΡœΏ–‘ΜΊΙιΖΫ≥ΧΩ…ΩΩΘ°

ΓΨΧβΡΩΓΩΡ≥ΙΛ≥ßΈΣΝΥΕ‘±ΨΙΛ≥ßΙΛ»ΥΒΡάμ¬έ≥…Φ®”κ ΒΦυΡήΝΠΫχ––Ζ÷ΈωΘ§ΨωΕ®¥”±ΨΙΛ≥ßΙΛ»Υ÷–ΥφΜζ≥ι»Γ“ΜΗω―υ±Ψ»ίΝΩΈΣ7ΒΡ―υ±ΨΫχ––Ζ÷ΈωΘ°»γΙϊΥφΜζ≥ι»ΓΒΡ7ΟϊΙΛ»ΥΒΡάμ¬έ≥…Φ®”κ ΒΦυΡήΝΠ÷Β![]() ΒΞΈΜΘΚΖ÷
ΒΞΈΜΘΚΖ÷![]() Ε‘”Π»γœ¬±μΘΚ
Ε‘”Π»γœ¬±μΘΚ
ΙΛ»Υ–ρΚ≈i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
άμ¬έ≥…Φ® | 60 | 65 | 70 | 75 | 85 | 87 | 90 |
ΒΦυΡήΝΠ÷Β | 70 | 77 | 80 | 85 | 90 | 86 | 93 |
Θ®1Θ©«σ’β7ΟϊΙΛ»ΥΒΡάμ¬έ≥…Φ®![]() ”κ ΒΦυΡήΝΠ÷Β
”κ ΒΦυΡήΝΠ÷Β![]() ΒΡ÷–ΈΜ ΐΓΔΦΪ≤νΘΜ
ΒΡ÷–ΈΜ ΐΓΔΦΪ≤νΘΜ
Θ®2Θ©»τΙφΕ®85Ζ÷“‘…œ![]() Αϋά®85Ζ÷
Αϋά®85Ζ÷![]() ΈΣ”≈–ψΘ§¥”’β7ΟϊΙΛ»Υ÷–≥ι»Γ3ΟϊΙΛ»ΥΘ§Φ«3ΟϊΙΛ»Υ÷–άμ¬έ≥…Φ®ΚΆ ΒΦυΡήΝΠ÷ΒΨυΈΣ”≈–ψΒΡ»Υ ΐΈΣXΘ§«σXΒΡΖ÷≤ΦΝ–ΚΆΤΎΆϊΘΜ
ΈΣ”≈–ψΘ§¥”’β7ΟϊΙΛ»Υ÷–≥ι»Γ3ΟϊΙΛ»ΥΘ§Φ«3ΟϊΙΛ»Υ÷–άμ¬έ≥…Φ®ΚΆ ΒΦυΡήΝΠ÷ΒΨυΈΣ”≈–ψΒΡ»Υ ΐΈΣXΘ§«σXΒΡΖ÷≤ΦΝ–ΚΆΤΎΆϊΘΜ
Θ®3Θ©ΗυΨίœ¬±μ ΐΨίΘ§«σ ΒΦυΡήΝΠ÷ΒyΙΊ”Ύάμ¬έ≥…Φ®xΒΡœΏ–‘ΜΊΙιΖΫ≥ΧΘ°![]() œΒ ΐΨΪ»ΖΒΫ
œΒ ΐΨΪ»ΖΒΫ![]()
ΗΫΘΚœΏ–‘ΜΊΙιΖΫ≥Χ![]() ÷–Θ§
÷–Θ§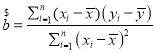 Θ§
Θ§![]() Θ°
Θ°
|
|
|
|
76 | 83 | 812 | 526 |
ΓΨΧβΡΩΓΩ’κΕ‘2019ΡξΓΑΥΪ °ΓΣΓ±Άχ…œΙΚΈοœϊΖ―«ιΩωΘ§ΙφΕ®ΘΚΥΪ °“ΜΒ±ΧλΙΚΈοœϊΖ―ΫπΕν≤ΜΒΆ”Ύ600‘ΣΒΡΆχΙΚ’ΏΈΣΓΑΕγ ÷Β≥Γ±Θ§ΒΆ”Ύ600‘ΣΒΡΆχΙΚ’ΏΈΣΓΑάμ÷«œϊΖ―’ΏΓ±.Ρ≥–Υ»Λ–ΓΉιΕ‘ΥΪ °“ΜΒ±ΧλΆχΙΚ’ΏΥφΜζ≥ι»ΓΝΥ100ΟϊΫχ––≥ι―υΖ÷ΈωΘ§ΒΟΒΫ»γœ¬Ά≥ΦΤΆΦ±μ(ΒΞΈΜΘΚ»Υ)ΘΚ
≈°–‘ | Ρ––‘ | ΉήΦΤ | |
Εγ ÷Β≥ | 50 | 5 | 55 |
άμ÷«ΙΚΈο’Ώ | 30 | 15 | 45 |
ΉήΦΤ | 80 | 20 | 100 |
Θ®1Θ©ΗυΨί“‘…œΆ≥ΦΤ ΐΨίΜΊ¥πΡήΖώ‘ΎΖΗ¥μΈσΒΡΗ≈¬ ≤Μ≥§Ιΐ0.010ΒΡ«ΑΧαœ¬»œΈΣΓΑΕγ ÷Β≥Γ±”κ–‘±π”–ΙΊΘΩ
Θ®2Θ©œ÷¥”≥ι»ΓΒΡ80Οϊ≈°–‘ΆχΙΚ’Ώ÷–Α¥’’Ζ÷≤ψ≥ι―υΒΡΖΫΖ®―Γ≥ω8»ΥΘ§»ΜΚσ¥”―Γ≥ω8»Υ÷–ΥφΜζ―Γ≥ω3»ΥΫχ––Βς≤ιΘ§―Γ≥ωΒΡΕγ ÷Β≥»Υ ΐΈΣ2 ±ΒΡΗ≈¬ .
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
≤ΈΩΦΙΪ ΫΘΚ Θ§Τδ÷–
Θ§Τδ÷–![]() .
.