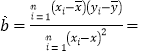题目内容
【题目】圆周上有![]() 个点
个点![]() ,用弦两两连结起来,其中任何3条弦都不在圆内共点.现将由此形成的互补重叠的圆内区域的个数记为
,用弦两两连结起来,其中任何3条弦都不在圆内共点.现将由此形成的互补重叠的圆内区域的个数记为![]() .
.
(1).直接画图求出![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;
;
(2).确定![]() 的表达式.
的表达式.
【答案】(1)见解析(2) ![]()
【解析】
(1)由下图可得![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
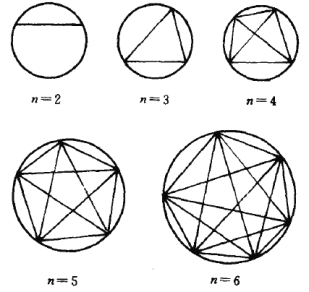
由前4个数值我们会猜测![]() ,但
,但![]() 否定了这个猜测.
否定了这个猜测.
(2)一般地,我们将所求区域分成两部分,一部分是![]() 个弓形,另一部分是多边形
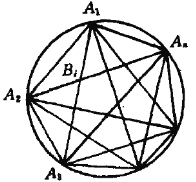
个弓形,另一部分是多边形![]() 内被对角线分成的区域.为叙述方便,我们将这些区域称为内区,而对角线交点(下图中
内被对角线分成的区域.为叙述方便,我们将这些区域称为内区,而对角线交点(下图中![]() )称为结点.
)称为结点.
考虑![]() 的情况(否则无结点,失去一般性)设多边形的内区中有
的情况(否则无结点,失去一般性)设多边形的内区中有![]() 个三角形,
个三角形,![]() 个四边形,
个四边形,![]() ,
,![]() 个
个![]() 边形,则
边形,则![]() 边形的内区有
边形的内区有![]() (个).
(个).
从而,![]() .
.
可见关键是求出![]() 来,分3步进行,
来,分3步进行,
(i)先计算各内区顶点总和的表达式.首先![]() .
.
由于多边形内每一个结点与多边形的4个顶点一一对应(如上图中![]() ,与
,与![]() ,
,![]() ,
,![]() ,
,![]() 对应),故结点共有
对应),故结点共有![]() 个,且每一内点对应着4个区域.而多边形的每一个顶点可引出
个,且每一内点对应着4个区域.而多边形的每一个顶点可引出![]() 条对角线,都是
条对角线,都是![]() 个三角形的公共点,因此,
个三角形的公共点,因此,![]() 又可表示为
又可表示为![]() ,
,
即![]() . ①
. ①
(ii)再计算各内区内角总和的表达式.首先
![]()
由于每一个内点都含有一个周角,总和为![]() .而
.而![]() 边形的每一个顶点上各角之和为
边形的每一个顶点上各角之和为![]() ,又有
,又有
![]()
对比![]() 的两种表达式得
的两种表达式得
![]() . ②
. ②
(iii)求出![]() ,进而得出
,进而得出![]() .
.
由①-②得
![]() .
.
从而,![]() .
.
这个式子也可以表示为
![]() . ③
. ③
若约定![]() ,则
,则![]() 的通项公式可用上述任一表达式.由于
的通项公式可用上述任一表达式.由于![]() ,
,
所以,③与④的前5项相同,![]() 时,猜想
时,猜想![]() 就不对了.
就不对了.

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目