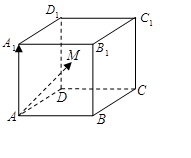题目内容
如图,在四棱锥P-ABCD中,底面ABCD是正方形,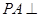 底面
底面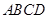 ,且PA=AB.
,且PA=AB.

(1)求证:BD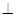 平面PAC;
平面PAC;
(2)求异面直线BC与PD所成的角.
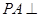 底面
底面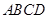 ,且PA=AB.
,且PA=AB.
(1)求证:BD
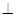 平面PAC;
平面PAC;(2)求异面直线BC与PD所成的角.
(1)根据线面垂直的判定定理来得到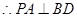 ,以及
,以及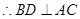 是解决的核心。
是解决的核心。
(2)45º.
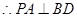 ,以及
,以及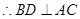 是解决的核心。
是解决的核心。(2)45º.
试题分析:(1)
证明:∵
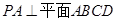 ,
,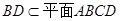 ,
,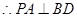 , 1分
, 1分又
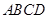 为正方形,
为正方形,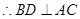 , 2分
, 2分而
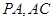 是平面
是平面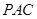 内的两条相交直线,
内的两条相交直线, 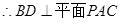 4分
4分(2)解: ∵
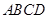 为正方形,
为正方形,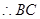 ∥
∥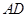 ,
,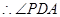 为异面直线
为异面直线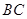 与
与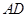 所成的角, 6分
所成的角, 6分由已知可知,△
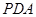 为直角三角形,又
为直角三角形,又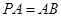 ,
,∵
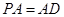 ,
, 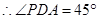 ,
,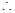 异面直线
异面直线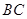 与
与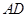 所成的角为45º. 8分
所成的角为45º. 8分点评:主要是考查了空间中线面的垂直的证明,以及异面直线所成的角的求解,属于基础题。

练习册系列答案
相关题目
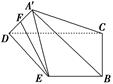
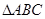 是边长为2的正三角形,
是边长为2的正三角形,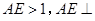 平面ABC,平面
平面ABC,平面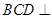 平面ABC,BD=CD,且
平面ABC,BD=CD,且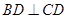 .
.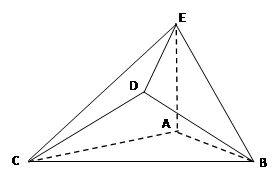
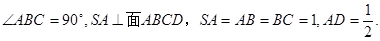
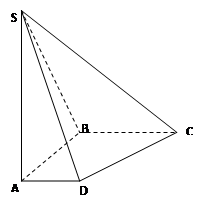
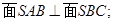
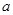 、
、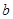 是两条不同的直线,
是两条不同的直线,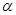 、
、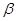 是两个不同的平面,则下列正确的个数为:( )
是两个不同的平面,则下列正确的个数为:( )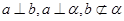 ,则
,则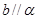 ; ②若
; ②若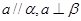 ,则
,则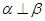 ;
;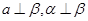 ,则
,则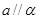 或
或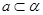 ;④若
;④若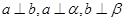 ,则
,则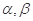 是两个不同的平面,则下列四个命题中是真命题的是( )
是两个不同的平面,则下列四个命题中是真命题的是( )



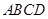 ,其边长为2,
,其边长为2,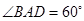 ,
,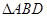 绕着
绕着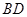 顺时针旋转
顺时针旋转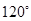 得到
得到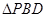 ,
,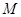 是
是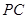 的中点.
的中点.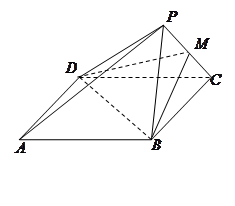
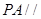 平面
平面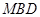 ;
;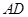 与平面
与平面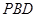 所成角的正弦值.
所成角的正弦值.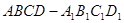 内(含正方体表面)任取一点
内(含正方体表面)任取一点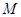 ,则
,则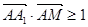 的概率
的概率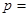 ( )
( )