题目内容
设 ,
, 满足
满足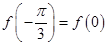 . (1)
求函数
. (1)
求函数 的单调递增区间;
的单调递增区间;
(2)设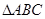 三内角
三内角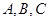 所对边分别为
所对边分别为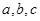 且
且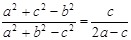 ,求
,求 在
在 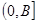 上的值域.
上的值域.
【答案】
(1)单调增区间为 ; (2)
; (2)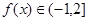 .
.
【解析】
试题分析:(1)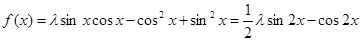
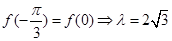
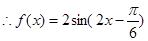 的单调增区间为
的单调增区间为 6分
6分
(2)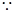
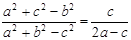 ,由余弦定理可变形为
,由余弦定理可变形为 ,由正弦定理为
,由正弦定理为
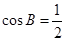
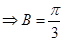
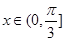
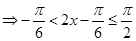
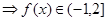 12分
12分
考点:本题主要考查三角函数的图象和性质,三角函数和差倍半公式,正弦定理、余弦定理的应用。
点评:典型题,三角函数的图象和性质、三角函数图象的变换是高考考查的重点,为研究三角函数的性质,往往要利用诱导公式、和差倍半公式进行“化一” 。(II)首先应用正弦定理、余弦定理确定B的范围,进一步研究指定角的范围内三角函数最大值、最小值问题。在确定角的范围时易出错,要特别细心。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,双曲线C1:
如图,双曲线C1: