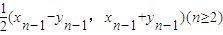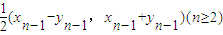题目内容
已知一非零向量列{| an |
| a1 |
| an |
| 1 |
| 2 |
(1)证明:{|
| an |
(2)设θn=?
| an |
| an |
分析:(1)先利用利用已知条件,利用向量的模的计算求得|
|=
|
|,根据等比数列的定义可推断出数列{|
|}是以
为首项,公比为
的等比数列
(2)利用向量的基本性质可求得cosθn的值,进而求得bn,最后利用等差数列的求和公式求得答案.
| an |
| ||
| 2 |
| an-1 |
| an |
| 2 |
| ||
| 2 |
(2)利用向量的基本性质可求得cosθn的值,进而求得bn,最后利用等差数列的求和公式求得答案.
解答:解:(l)∵|
|=
=
=
|
-1|(n≥2),
又|
|=
∴数列{|
|}是以
为首项,公比为
的等比数列.
(2)∵
-1•
=(xn-1•yn-1)•
(xn-1-yn-1•xn-1+yn-1)=
(
+
)=
|
-1|2
∴cosθn=
=
,∴θn=?
-1,
>=
,∴bn=2nθn-1=
-1Sn=b1+b2++bn=(
-1)+(
-1)++(
-1)=
(n2+n)-n
| an |
| 1 |
| 2 |
| (xn-1-yn-1)2+(xn-1+yn-1)2 |
| ||
| 2 |
x2n-1+
|
| ||
| 2 |
| an |
又|
| a1 |
| 2 |
∴数列{|
| an |
| 2 |
| ||
| 2 |
(2)∵
| an |
| an |
| 1 |
| 2 |
| 1 |
| 2 |
| x | 2 n-1 |
| y | 2 n-1 |
| 1 |
| 2 |
| an |
∴cosθn=
| ||||
|
|
| ||
| 2 |
| an |
| an |
| π |
| 4 |
| nπ |
| 2 |
| π |
| 2 |
| 2π |
| 2 |
| nπ |
| 2 |
| π |
| 4 |
点评:本题主要考查了等比数列的确定.考查了学生对数列基础知识的灵活运用.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目