题目内容
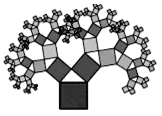
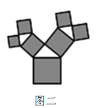
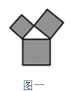
【题目】如图是美丽的“勾股树”，它是一个直角三角形分别以它的每一边向外作正方形而得到.图一是第1代“勾股树”，重复图一的作法，得到图二为第2代“勾股树”，以此类推，已知最大的正方形面积为1，则第n代“勾股树”所有正方形的面积的和为（ ）
A. nB. 
C. 
D. 
【答案】C
【解析】
根据题中所给的条件，最大的正方形的面积为1，从而得到直角三角形的斜边长为1，两个直角边的平方和为1，从而得到图一的三个正方形面积和为2，再算出图二的“勾股树”的所有正方形的面积和为3，观察各选项中的式子求得结果.
最大的正方形的面积为1，
当
时，由勾股定理知正方形面积的和为2，
当
时，从图二中图形的特征，
结合勾股定理以及正方形的面积公式，
求得图二的“勾股树”的所有正方形的面积和为3，
即当时，勾股树的面积为为3，
由此类推，并结合选项，可以得出所有正方形面积的和为
，
故选D.
【题目】铁人中学高二学年某学生对其亲属30人
饮食习惯进行了一次调查，并用如图所示的茎叶图表示30人的饮食指数．（说明：图中饮食指数低于70的人，饮食以蔬菜为主；饮食指数高于70的人，饮食以肉类为主．）
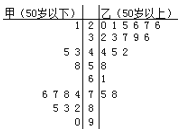
（Ⅰ）根据茎叶图，帮助这位学生说明其亲属30人的饮食习惯；
（Ⅱ）根据以上数据完成下列
的列联表：
主食蔬菜 | 主食肉类 | 合计 | |
50岁以下人数 | |||
50岁以上人数 | |||
合计人数 |
（Ⅲ）能否在犯错误的概率不超过0.01的前提下认为其亲属的饮食习惯与年龄有关系？
附：
.
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】某位同学进行寒假社会实践活动，为了对白天平均气温与某奶茶店的某种饮料销量之间的关系进行分析研究，他分别记录了1月11日至1月15日的白天平均气温
与该小卖部的这种饮料销量
（杯），得到如下数据：
日期 | 1月11日 | 1月12日 | 1月13日 | 1月14日 | 1月15日 |
平均气温 | 9 | 10 | 12 | 11 | 8 |
销量 | 23 | 25 | 30 | 26 | 21 |
（1）若先从这五组数据中抽出2组，求抽出的2组数据恰好是相邻2天数据的概率；
（2）请根据所给五组数据，求出关于
的线性回归方程
；
（3）根据（1）中所得的线性回归方程，若天气预报1月16日的白天平均气温
，请预测该奶茶店这种饮料的销量.
（参考公式：
，
）
【题目】针对国家提出的延迟退休方案，某机构进行了网上调查，所有参与调查的人中，持“支持”、“保留”和“不支持”态度的人数如下表所示：
| 支持 | 保留 | 不支持 |
|
|
|
|
|
|
|
|
（1）在所有参与调查的人中，用分层抽样的方法抽取
个人，已知从持“不支持”态度的人中抽取了
人，求
的值；
（2）在持“不支持”态度的人中，用分层抽样的方法抽取
人看成一个总体，从这
人中任意选取
人，求
岁以下人数
的分布列和期望；
（3）在接受调查的人中，有
人给这项活动打出的分数如下： 
， 
， 
， 
， 
， 
， 
， 
， 
， 
，把这
个人打出的分数看作一个总体，从中任取一个数，求该数与总体平均数之差的绝对值超过
概率.