题目内容
已知函数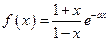 。
。
(Ⅰ)设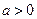 ,讨论
,讨论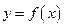 的单调性;
的单调性;
(Ⅱ)若对任意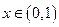 恒有
恒有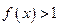 ,求
,求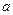 的取值范围。
的取值范围。
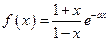 。
。(Ⅰ)设
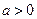 ,讨论
,讨论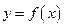 的单调性;
的单调性;(Ⅱ)若对任意
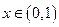 恒有
恒有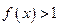 ,求
,求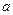 的取值范围。
的取值范围。(Ⅰ)f(x)在(-∞, -), (,1), (1,+∞)为增函数, f(x)在(-,)为减函数;(Ⅱ)a∈(-∞,2]时,对任意x∈(0,1)恒有f(x)>1。
(Ⅰ)f(x)的定义域为(-∞,1)∪(1,+∞).对f(x)求导数得 f '(x)= e-ax.
(ⅰ)当a=2时, f '(x)= e-2x, f '(x)在(-∞,0), (0,1)和(1,+ ∞)均大于0,
所以f(x)在(-∞,1), (1,+∞).为增函数.
(ⅱ)当0<a<2时, f '(x)>0, f(x)在(-∞,1), (1,+∞)为增函数.
(ⅲ)当a>2时, 0<<1, 令f '(x)="0" ,解得x1= - , x2= .
当x变化时, f '(x)和f(x)的变化情况如下表:
f(x)在(-∞, -), (,1), (1,+∞)为增函数,
f(x)在(-,)为减函数.
(Ⅱ)(ⅰ)当0<a≤2时, 由(Ⅰ)知: 对任意x∈(0,1)恒有f(x)>f(0)=1.
(ⅱ)当a>2时, 取x0= ∈(0,1),则由(Ⅰ)知 f(x0)<f(0)=1
(ⅲ)当a≤0时, 对任意x∈(0,1),恒有 >1且e-ax≥1,得
f(x)= e-ax≥ >1. 综上当且仅当a∈(-∞,2]时,对任意x∈(0,1)恒有f(x)>1.
(ⅰ)当a=2时, f '(x)= e-2x, f '(x)在(-∞,0), (0,1)和(1,+ ∞)均大于0,
所以f(x)在(-∞,1), (1,+∞).为增函数.
(ⅱ)当0<a<2时, f '(x)>0, f(x)在(-∞,1), (1,+∞)为增函数.
(ⅲ)当a>2时, 0<<1, 令f '(x)="0" ,解得x1= - , x2= .
当x变化时, f '(x)和f(x)的变化情况如下表:
| x | (-∞, -) | (-,) | (,1) | (1,+∞) |
| f '(x) | + | - | + | + |
| f(x) | ↗ | ↘ | ↗ | ↗ |
f(x)在(-,)为减函数.
(Ⅱ)(ⅰ)当0<a≤2时, 由(Ⅰ)知: 对任意x∈(0,1)恒有f(x)>f(0)=1.
(ⅱ)当a>2时, 取x0= ∈(0,1),则由(Ⅰ)知 f(x0)<f(0)=1
(ⅲ)当a≤0时, 对任意x∈(0,1),恒有 >1且e-ax≥1,得
f(x)= e-ax≥ >1. 综上当且仅当a∈(-∞,2]时,对任意x∈(0,1)恒有f(x)>1.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
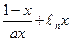 在[1,+∞
在[1,+∞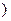 上为增函数.
上为增函数.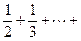
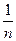
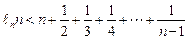 (n∈N*且n ≥ 2 )
(n∈N*且n ≥ 2 )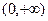 上的函数
上的函数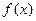 满足下面三个条件:
满足下面三个条件: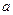 、
、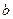 ,都有
,都有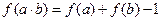 ; ②
; ②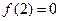 ;
;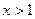 时,总有
时,总有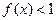 .
.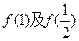 的值;
的值;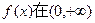 上是减函数.
上是减函数. 的最小值为0,
的最小值为0,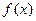 的最大值及此时x的集合。
的最大值及此时x的集合。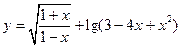 的定义域为
的定义域为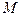 ,
,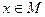 时,求
时,求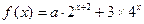
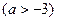 的最小值.
的最小值.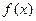 在
在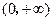 上为增函数,且
上为增函数,且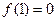 ,则不等式
,则不等式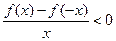 的解集为( )
的解集为( )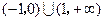
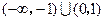
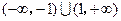
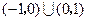
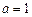 时,求所有使
时,求所有使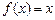 成立的
成立的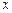 的值;
的值;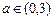 时,求函数
时,求函数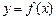 在闭区间
在闭区间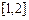 上的最小值;
上的最小值;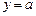 的交点个数
的交点个数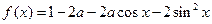 的最小值为
的最小值为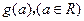
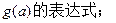 (2)若
(2)若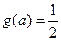 ,求
,求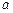 及此时
及此时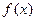 的最大值
的最大值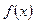 是R上的偶函数,且在区间
是R上的偶函数,且在区间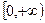 上是增函数.令
上是增函数.令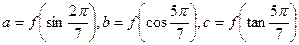 ,则
,则