题目内容
(2004•朝阳区一模)(Ⅰ)解关于x的不等式(lgx)2-lgx-2>0;
(Ⅱ)若不等式(lgx)2-(2+m)lgx+m-1>0对于|m|≤1恒成立,求x的取值范围.
(Ⅱ)若不等式(lgx)2-(2+m)lgx+m-1>0对于|m|≤1恒成立,求x的取值范围.
分析:(I)把lgx看作一个整体(未知数),此不等式是关于lgx的一元二次不等式,先解出lgx的取值范围,进而利用对数函数的单调性即可得出x的取值范围;
(II)设y=lgx,则原不等式可化为y2-(2+m)y+m-1>0,y2-2y-my+m-1>0.即(1-y)m+(y2-2y-1)>0.当y=1时,不等式不成立.设f(m)=(1-y)m+(y2-2y-1),则f(x)是m的一次函数,利用一次函数的单调性即可解出.
(II)设y=lgx,则原不等式可化为y2-(2+m)y+m-1>0,y2-2y-my+m-1>0.即(1-y)m+(y2-2y-1)>0.当y=1时,不等式不成立.设f(m)=(1-y)m+(y2-2y-1),则f(x)是m的一次函数,利用一次函数的单调性即可解出.
解答:解:(Ⅰ)∵(lgx)2-lgx-2>0,
∴(lgx+1)(lgx-2)>0.
∴lgx<-1或lgx>2.
∴0<x<
或x>102.
(Ⅱ)设y=lgx,则原不等式可化为y2-(2+m)y+m-1>0,∴y2-2y-my+m-1>0.
∴(1-y)m+(y2-2y-1)>0.
当y=1时,不等式不成立.
设f(m)=(1-y)m+(y2-2y-1),则f(x)是m的一次函数,且一次函数为单调函数.
当-1≤m≤1时,若要f(m)>0?
?
?
?
则y<-1或y>3.
∴lgx<-1或lgx>3.
∴0<x<
或x>103.
∴x的取值范围是(0,
)∪(103,+∞).
∴(lgx+1)(lgx-2)>0.
∴lgx<-1或lgx>2.
∴0<x<
| 1 |
| 10 |
(Ⅱ)设y=lgx,则原不等式可化为y2-(2+m)y+m-1>0,∴y2-2y-my+m-1>0.
∴(1-y)m+(y2-2y-1)>0.
当y=1时,不等式不成立.
设f(m)=(1-y)m+(y2-2y-1),则f(x)是m的一次函数,且一次函数为单调函数.
当-1≤m≤1时,若要f(m)>0?
|
|
|
|
∴lgx<-1或lgx>3.
∴0<x<
| 1 |
| 10 |
∴x的取值范围是(0,
| 1 |
| 10 |
点评:熟练掌握换元法、等价转化法、一元二次不等式的解法、一次函数的单调性是解题的关键.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
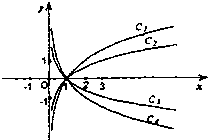 (2004•朝阳区一模)已知图中曲线C1、C2、C3、C4是函数logax的图象,则曲线C1、C2、C3、C4对应的a的值依次为( )
(2004•朝阳区一模)已知图中曲线C1、C2、C3、C4是函数logax的图象,则曲线C1、C2、C3、C4对应的a的值依次为( )