题目内容
（2004•朝阳区一模）若三棱锥S-ABC的顶点S在底面上的射影H在△ABC的内部，且是△ABC的垂心，则（ ）
分析：根据条件“三棱锥S-ABC的顶点S在底面的射影H是△ABC的垂心”可以得到此三棱锥的三条相对的棱两两垂直，过任一个顶点向对面作垂线，根据线面垂直的性质定理可得到垂足是对面的三角形的高线的交点，从而得到垂心．
解答：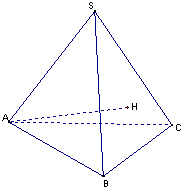
解：∵三棱锥S-ABC的顶点S在底面的射影H是△ABC的垂心，
∴三棱锥的三条相对的棱两两垂直，
反之，若三棱锥的三条相对的棱两两垂直，
则有三棱锥任意一个顶点在对面的射影是对面三角形的垂心，
过顶点A向平面SBC作垂线，垂足为H，如图，
根据线面垂直的性质定理，得到垂足H是△SBC的高线的交点，
∴点A在平面SBC上的射影必是△SBC的垂心，
故选D．
解：∵三棱锥S-ABC的顶点S在底面的射影H是△ABC的垂心，∴三棱锥的三条相对的棱两两垂直，
反之，若三棱锥的三条相对的棱两两垂直，
则有三棱锥任意一个顶点在对面的射影是对面三角形的垂心，
过顶点A向平面SBC作垂线，垂足为H，如图，
根据线面垂直的性质定理，得到垂足H是△SBC的高线的交点，
∴点A在平面SBC上的射影必是△SBC的垂心，
故选D．
点评：本题考查三角形的垂心，考查棱锥的结构特征，是一个比较简单的综合题目．
练习册系列答案
阅读快车系列答案
相关题目
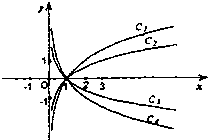（2004•朝阳区一模）已知图中曲线C1、C2、C3、C4是函数logax的图象，则曲线C1、C2、C3、C4对应的a的值依次为（ ）