题目内容
(2004•朝阳区一模)设a=
cos6°-
sin6°,b=
,c=
,则有( )
| 1 |
| 2 |
| ||
| 2 |
| 2tan13° |
| 1-tan213° |
|
分析:由辅助角公式和两角差的正弦公式算出a=sin24°,由二倍角的正切公式算出b=tan26°,再由二倍角的余弦公式化简出c=sin65°.然后结合特殊角的三角函数值和同角三角函数的关系,对a、b、c分别加以比较,可得a<b<c.
解答:解:a=
cos6°-
sin6°=sin30°cos6°-cos30°sin6°=sin(30°-6°)=sin24°,
b=
=tan26°,c=
=
=cos25°=sin65°,
∵sin24°<
=tan24°,而tan24°<tan26°,∴a<b
又∵tan26°<tan30°=
,而sin65°>sin60°=
∴tan26°<sin65°,可得b<c
综上所述,可得a<b<c
故选:B
| 1 |
| 2 |
| ||
| 2 |
b=
| 2tan13° |
| 1-tan213° |
|
|
∵sin24°<
| sin24° |
| cos24° |
又∵tan26°<tan30°=
| ||
| 3 |
| ||
| 2 |
∴tan26°<sin65°,可得b<c
综上所述,可得a<b<c
故选:B
点评:本题给出3个三角函数式分别记为a、b、c,比较a、b、c的大小关系,着重考查了同角三角函数的关系、特殊角的三角函数值和二倍角公式等知识,属于中档题.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
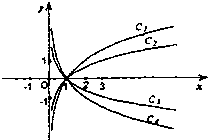 (2004•朝阳区一模)已知图中曲线C1、C2、C3、C4是函数logax的图象,则曲线C1、C2、C3、C4对应的a的值依次为( )
(2004•朝阳区一模)已知图中曲线C1、C2、C3、C4是函数logax的图象,则曲线C1、C2、C3、C4对应的a的值依次为( )