题目内容
(2004•朝阳区一模)过双曲线(x-2)2-
=1的右焦点作直线l交双曲线于A、B两点,如果|AB|=4,则这样的直线的条数为( )
| y2 |
| 2 |
分析:可先设带参数的直线l2的方程,再代入双曲线方程,用弦长公式求出长度,与所给长度4相等,可求出参数的值,由参数的个数可得答案.
解答:解:直线l2过右焦点为F(2+
,0),可设直线l2的方程为x=my+2+
代入(x-2)2-
=1,
得(2m2-1)y2+4
my+4=0,
设M(x1,y1),N(x2,y2)
则y1+y2=-
,y1y2=
,
∴|y1-y2|=
,
故|MN|=
•|y1-y2|=
,
∴
=4,解得:m=0或m=±
,
故这样的直线有3条,
故选C.
| 3 |
| 3 |
| y2 |
| 2 |
得(2m2-1)y2+4
| 3 |
设M(x1,y1),N(x2,y2)
则y1+y2=-
4
| ||
| 2m2-1 |
| 4 |
| 2m2-1 |
∴|y1-y2|=
4
| ||
| |2m2-1| |
故|MN|=
| m2-1 |
| 4(m2+1) |
| |2m2-1| |
∴
| 4(m2+1) |
| |2m2-1| |
| 2 |
故这样的直线有3条,
故选C.
点评:本题主要考查直线与双曲线的位置关系、弦长公式、韦达定理等知识,考查方程思想.

练习册系列答案
相关题目
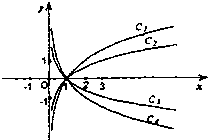 (2004•朝阳区一模)已知图中曲线C1、C2、C3、C4是函数logax的图象,则曲线C1、C2、C3、C4对应的a的值依次为( )
(2004•朝阳区一模)已知图中曲线C1、C2、C3、C4是函数logax的图象,则曲线C1、C2、C3、C4对应的a的值依次为( )