题目内容
5.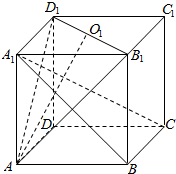 已知点O1是正方体ABCD-A1B1C1D1的上底面的中心,求证:对角线A1C与平面AD1B1的交点P一定在AO1上.
已知点O1是正方体ABCD-A1B1C1D1的上底面的中心,求证:对角线A1C与平面AD1B1的交点P一定在AO1上.
分析 由已知条件利用公理三得面AA1D1∩平面AA1C1C=AO1,且P∈平面AA1C1C,P∈平面AB1D1,由此利用公理三能证明对角线A1C与平面AD1B1的交点P一定在AO1上.
解答  证明:连结A1C1,AC,
证明:连结A1C1,AC,
∵O1是正方体ABCD-A1B1C1D1的上底面的中心,
∴O1∈A1C1,且O1∈B1D1,
∵A1C1?平面AA1C1C,B1D1?平面AB1D1,
∴O1∈平面AA1C1C,O1∈平面AB1D1,
又∵A∈平面AA1C1C,A∈平面AB1D1,
∴面AA1D1∩平面AA1C1C=AO1,
∵对角线A1C∩平面AD1B1=P,
∴P∈平面AA1C1C,P∈平面AB1D1,
∴公理三得对角线A1C与平面AD1B1的交点P一定在AO1上.
点评 本题考查点在直线上的证明,是基础题,解题时要认真审题,注意公理三的合理运用.

练习册系列答案
相关题目
20.下列说法中,正确的是( )
| A. | 集合{x|x∈Z,|x|<2}的非空真子集的个数是7 | |
| B. | 函数y=($\frac{1}{2}$)${\;}^{{x}^{2}-3x+2}$的单调递减区间是(-∞,$\frac{3}{2}$] | |
| C. | 已知函数f(x)是定义在R上的奇函数,当x∈(-∞,0)时,f(x)=x-x4,则当x∈(0,+∞)时,f(x)=-x-x4 | |
| D. | 已知f($\frac{2}{x}$+1)=x+3,则f(x)=$\frac{3x-1}{x-1}$ |
14.已知向量$\overrightarrow{a}$=(sinθ,-2)与$\overrightarrow{b}$=(1,cosθ)互相垂直,其中θ∈$(0,\frac{π}{2})$,则sinθ+cosθ等于( )
| A. | $\frac{{-\sqrt{5}}}{5}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{{2\sqrt{5}}}{5}$ | D. | $\frac{{3\sqrt{5}}}{5}$ |