题目内容
10.若过抛物线x2=4y的准线上一动点P作此抛物线的两条切线,切点分别为A(x1,y1)、B(x2,y2);点O为坐标原点.则以下命题(1)直线AB过定点;
(2)∠AOB为钝角;
(3)∠APB可取60°;
(4)若△ABO的面积为$\frac{5}{2}$,则点P坐标为($\frac{3}{2}$,-1)或(-$\frac{3}{2}$,-1).
其中正确的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 (1)求出导数,求得切线的斜率,求得切线PA,PB的方程,代入P的坐标整理,可得AB的方程,即可得到恒过定点;
(2)由PA,PB的方程,可得x1,x2是方程$\frac{1}{4}$x2-$\frac{1}{2}$x0x-1=0的两根,运用韦达定理和向量的数量积,即可判断;
(3)取AB中点Q,连PQ,再作AA1⊥l于A1,BB1⊥l于B1,运用抛物线的定义和梯形的中位线定理,结合直角三角形的性质,即可判断;
(4)由(1)知直线AB的方程为y=$\frac{1}{2}$t+1,恒过定点F(0,1),利用分割法表示出三角形的面积,结合根与系数之间的关系进行求解即可.
解答 解:(1)y=$\frac{1}{4}$x2,导数y′=$\frac{1}{2}$x,切线PA的方程:y-y1=$\frac{1}{2}$x1(x-x1),
由于y1=$\frac{1}{4}$x12,PA过P(x0,-1),y1-$\frac{1}{2}$x0x1-1=0,
同理y2-$\frac{1}{2}$x0x2-1=0,A,B坐标都适合方程y-$\frac{1}{2}$x0x-1=0,
过A,B的方程为y-$\frac{1}{2}$x0x-1=0,恒过定点F(0,1),故(1)正确;
(2)y1=$\frac{1}{4}$x12,PA过P(x0,-1),即有$\frac{1}{4}$x12-$\frac{1}{2}$x0x1-1=0,同理可得$\frac{1}{4}$x22-$\frac{1}{2}$x0x2-1=0,
x1,x2是方程$\frac{1}{4}$x2-$\frac{1}{2}$x0x-1=0的两根,即有x1+x2=2x0,x1x2=-4.
由$\overrightarrow{OA}$•$\overrightarrow{OB}$=x1x2+$\frac{1}{16}$(x1x2)2=-4+$\frac{1}{16}$×16=-3<0,即有∠AOB为钝角,故(2)正确;
(3)取AB中点Q,连PQ,再作AA1⊥l于A1,BB1⊥l于B1,由(2)可知P为A1B1的中点,
由抛物线的定义可得AA1=AF,BB1=BF,PQ=$\frac{1}{2}$(AA1+BB1)=$\frac{1}{2}$(AF+BF)=$\frac{1}{2}$AB,
即有∠APB=90°,故(3)错;
(4)设P(t,-1),由(1)知,直线AB的方程为y=$\frac{1}{2}$t+1,恒过定点F(0,1),
若S△AB0=$\frac{5}{2}$,不妨设x2>x1,
则S△AB0=S△A0F+S△B0F=$\frac{1}{2}$|OF|•|x1|+$\frac{1}{2}$|OF|•|x2|=$\frac{1}{2}$(x2-x1)=$\frac{5}{2}$,
则x2-x1=5,
由y=$\frac{1}{2}$t+1代入x2=4y,得x2-2tx-4=0,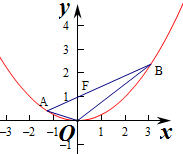
则x2+x1=2t,x2x1=-4,
则(x2-x1)2=(x2+x12)-4x2x1,
即4t2+16=25,
即t2=$\frac{9}{4}$,解得t=±$\frac{3}{2}$,
此时点P的坐标为是($\frac{3}{2}$,-1)或(-$\frac{3}{2}$,-1).故(4)正确.
故正确的个数为3.
故选:C.
点评 本题考查抛物线的定义、方程和性质,考查直线恒过定点的求法以及运用向量的数量积判断夹角的大小,注意平面几何的运用,难度较大.

| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
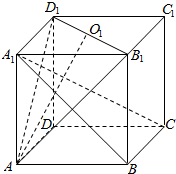 已知点O1是正方体ABCD-A1B1C1D1的上底面的中心,求证:对角线A1C与平面AD1B1的交点P一定在AO1上.
已知点O1是正方体ABCD-A1B1C1D1的上底面的中心,求证:对角线A1C与平面AD1B1的交点P一定在AO1上.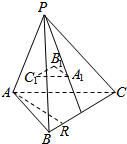 如图,P是△ABC所在平面外的一点,A1,B1,C1依次是△PBC,△PAC,△PAB的重心,AR是平面ABC内的任意一条直线,求证:AR∥平面A1B1C1.
如图,P是△ABC所在平面外的一点,A1,B1,C1依次是△PBC,△PAC,△PAB的重心,AR是平面ABC内的任意一条直线,求证:AR∥平面A1B1C1.