题目内容
16.已知|$\overrightarrow{a}$-t$\overrightarrow{e}$|≥|$\overrightarrow{a}$-$\overrightarrow{e}$|,且$\overrightarrow{a}$≠$\overrightarrow{e}$,求$\overrightarrow{a}$•$\overrightarrow{e}$.分析 |$\overrightarrow{a}$-t$\overrightarrow{e}$|≥|$\overrightarrow{a}$-$\overrightarrow{e}$|,且$\overrightarrow{a}$≠$\overrightarrow{e}$,两边平方化为t2-$2t\overrightarrow{a}•\overrightarrow{e}$+$2\overrightarrow{a}•\overrightarrow{e}$-1≥0恒成立,可得△≤0,解出即可.
解答 解:∵|$\overrightarrow{a}$-t$\overrightarrow{e}$|≥|$\overrightarrow{a}$-$\overrightarrow{e}$|,且$\overrightarrow{a}$≠$\overrightarrow{e}$,
∴${\overrightarrow{a}}^{2}-2t\overrightarrow{a}•\overrightarrow{e}$+${t}^{2}{\overrightarrow{e}}^{2}$≥${\overrightarrow{a}}^{2}$-2$\overrightarrow{a}•\overrightarrow{e}$+${\overrightarrow{e}}^{2}$,
化为t2-$2t\overrightarrow{a}•\overrightarrow{e}$+$2\overrightarrow{a}•\overrightarrow{e}$-1≥0恒成立,
∴△=$4(\overrightarrow{a}•\overrightarrow{e})^{2}$-4($2\overrightarrow{a}•\overrightarrow{e}$-1)≤0,
化为$(\overrightarrow{a}•\overrightarrow{e}-1)^{2}≤$0,
∴$\overrightarrow{a}$•$\overrightarrow{e}$=1.
点评 本题考查了向量数量积运算性质、二次函数的性质、一元二次不等式的解集与判别式的关系,考查了推理能力与计算能力,属于中档题.

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案| A. | $\frac{b}{a}$ | B. | $\frac{a}{b}$ | C. | ab | D. | ba |
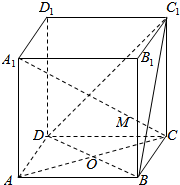 已知在正方体ABCD-A1B1C1D1中,O是DB的中点,直线A1C交平面C1BD于点M,判断下列结论是否正确:
已知在正方体ABCD-A1B1C1D1中,O是DB的中点,直线A1C交平面C1BD于点M,判断下列结论是否正确: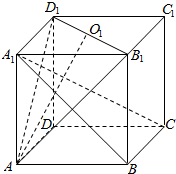 已知点O1是正方体ABCD-A1B1C1D1的上底面的中心,求证:对角线A1C与平面AD1B1的交点P一定在AO1上.
已知点O1是正方体ABCD-A1B1C1D1的上底面的中心,求证:对角线A1C与平面AD1B1的交点P一定在AO1上.