题目内容
【题目】对于四面体ABCD,以下命题中,真命题的序号为(填上所有真命题的序号)
①若AB=AC,BD=CD,E为BC中点,则平面AED⊥平面ABC;
②若AB⊥CD,BC⊥AD,则BD⊥AC;
③若所有棱长都相等,则该四面体的外接球与内切球的半径之比为2:1;
④若以A为端点的三条棱所在直线两两垂直,则A在平面BCD内的射影为△BCD的垂心;
⑤分别作两组相对棱中点的连线,则所得的两条直线异面.
【答案】①②④
【解析】解:如图,对于①,∵AB=AC,BD=CD,E为BC中点,
∴AE⊥BC,DE⊥BC,
又AE∩ED=E,
∴BC⊥面AED,
∴面AED⊥平面ABC.
∴命题①正确;
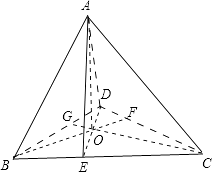
对于②,过A作底面BCD的垂线AO,垂足为O,
连结BO并延长交CD于F,连结DO并延长交BC于E,
由线面垂直的判定可以证明BF⊥CD,DE⊥BC,从而可知O为底面三角形的垂心,
连结CO并延长交BD于G,则CG⊥BD,再由线面垂直的判断得到BD⊥面ACG,从而得到BD⊥AC.
∴命题②正确;
对于③,若所有棱长都相等,四面体为正四面体,该四面体的外接球半径是四面体高的四分之三,
内切球的半径是四面体高的四分之一,∴该四面体的外接球与内切球的半径之比为3:1.
∴命题③错误;
对于④,若AB⊥AC⊥AD,过A作底面BCD的垂线AO,垂足为O,
由AB⊥AC,AB⊥AD,且AC∩AD=A,得AB⊥面ACD,则AB⊥CD,进一步由线面垂直的判定证得CD⊥面ABO,
则BO⊥CD,同理可证CO⊥BD,说明O为△BCD的垂心.命题④正确;
对于⑤,如图,
∵E、F、G、H分别为BC、AC、BD、AD的中点,
∴HF∥DC,GE∥DC,
∴EFHG为平面四边形.
∴命题⑤错误.
∴真命题的序号是①②④.
所以答案是:①②④.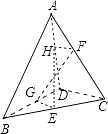
【考点精析】根据题目的已知条件,利用命题的真假判断与应用和异面直线的判定的相关知识可以得到问题的答案,需要掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系;过平面外一点与平面内一点的直线和平面内不经过该点的直线是异面直线.(不在任何一个平面内的两条直线).

 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案【题目】某单位有车牌尾号为![]() 的汽车
的汽车![]() 和尾号为
和尾号为![]() 的汽车
的汽车![]() ,两车分属于两个独立业务部分.对一段时间内两辆汽车的用车记录进行统计,在非限行日,
,两车分属于两个独立业务部分.对一段时间内两辆汽车的用车记录进行统计,在非限行日, ![]() 车日出车频率
车日出车频率![]() ,
, ![]() 车日出车频率
车日出车频率![]() .该地区汽车限行规定如下:
.该地区汽车限行规定如下:
车尾号 |
|
|
|
|
|
限行日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
现将汽车日出车频率理解为日出车概率,且![]() ,
, ![]() 两车出车相互独立.
两车出车相互独立.
(I)求该单位在星期一恰好出车一台的概率.
(II)设![]() 表示该单位在星期一与星期二两天的出车台数之和,求
表示该单位在星期一与星期二两天的出车台数之和,求![]() 的分布列及其数学期望
的分布列及其数学期望![]() .
.