题目内容
3.已知B,C是球O的一个小圆O1上的两点,且BC=2$\sqrt{3}$,∠BOC=$\frac{π}{2}$,∠BO1C=$\frac{2π}{3}$,则三棱锥O-O1BC的体积为$\frac{\sqrt{6}}{3}$.分析 由题意,OO1⊥平面O1BC,求出球O,小圆O1的半径,即可求出三棱锥O-O1BC的体积.
解答 解:由题意,OO1⊥平面O1BC.
因为BC=2$\sqrt{3}$,∠BOC=$\frac{π}{2}$,∠BO1C=$\frac{2π}{3}$,
所以OB=$\sqrt{6}$,O1C=2,
所以OO1=$\sqrt{2}$,
所以三棱锥O-O1BC的体积为$\frac{1}{3}×\frac{1}{2}×2×2×\sqrt{2}$×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{6}}{3}$.
故答案为:$\frac{\sqrt{6}}{3}$.
点评 本题考查三棱锥O-O1BC的体积,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
14.设x>0,y>0,A=$\frac{x+y}{1+x+y}$,B=$\frac{x}{1+x}+\frac{y}{1+y}$,则A与B的大小关系为( )
| A. | A>B | B. | A≥B | C. | A<B | D. | A≤B |
8.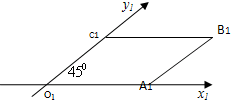 如图,一个正方形OABC在斜二测画法下的直观图是个一条边长为1的平行四边形,则正方形OABC的面积为( )
如图,一个正方形OABC在斜二测画法下的直观图是个一条边长为1的平行四边形,则正方形OABC的面积为( )
 如图,一个正方形OABC在斜二测画法下的直观图是个一条边长为1的平行四边形,则正方形OABC的面积为( )
如图,一个正方形OABC在斜二测画法下的直观图是个一条边长为1的平行四边形,则正方形OABC的面积为( )| A. | 1 | B. | 4 | C. | 1或4 | D. | 不能确定 |
 如图△ABC内接于圆O,AB=AC,直线MN切圆O于点C,弦BD∥MN,AC与BD相交于点E.
如图△ABC内接于圆O,AB=AC,直线MN切圆O于点C,弦BD∥MN,AC与BD相交于点E. 把正奇数数列{2n-1}中的数按上小下大、左小右大的原则排成如图的三角形数表:
把正奇数数列{2n-1}中的数按上小下大、左小右大的原则排成如图的三角形数表: 在电脑游戏中,“主角”的生命机会往往被预先设定.如某枪战游戏,“主角”被设置生命6次,每次生命承受射击8次(即被击中8次就失去一次生命机会),假设射击为单发射击,如图是为“主角”耗用生命机会的过程设计的一个程序框图,请问判断框内应该填( )
在电脑游戏中,“主角”的生命机会往往被预先设定.如某枪战游戏,“主角”被设置生命6次,每次生命承受射击8次(即被击中8次就失去一次生命机会),假设射击为单发射击,如图是为“主角”耗用生命机会的过程设计的一个程序框图,请问判断框内应该填( )