题目内容
14.设x>0,y>0,A=$\frac{x+y}{1+x+y}$,B=$\frac{x}{1+x}+\frac{y}{1+y}$,则A与B的大小关系为( )| A. | A>B | B. | A≥B | C. | A<B | D. | A≤B |
分析 通过A、B分离常数1,直接利用放缩法推出所求结果.
解答 解:A=$\frac{x+y}{1+x+y}$=1-$\frac{1}{1+x+y}$,
B=$\frac{x}{1+x}+\frac{y}{1+y}$=$\frac{x+2xy+y}{(1+x)(1+y)}$=1-$\frac{1-xy}{1+x+y+xy}$,
∵$\frac{1-xy}{1+x+y+xy}$<$\frac{1}{1+x+y+xy}$<$\frac{1}{1+x+y}$,
∴-$\frac{1}{1+x+y}$<-$\frac{1-xy}{1+x+y+xy}$,
∴A<B,
故选:C.
点评 本题考查了不等式大小比较的方法,属于基础题.

练习册系列答案
相关题目
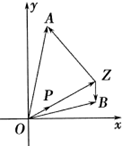 如图,已知$\overrightarrow{OP}$=(2,1),$\overrightarrow{OA}$=(1,7),$\overrightarrow{OB}$=(5,1),设Z是直线OP上的一动点.
如图,已知$\overrightarrow{OP}$=(2,1),$\overrightarrow{OA}$=(1,7),$\overrightarrow{OB}$=(5,1),设Z是直线OP上的一动点.