Question

11．已知$\overrightarrow{OA}=\overrightarrow a，\overrightarrow{OB}$=$\overrightarrow b$，$\overrightarrow a$与$\overrightarrow b$不共线，任意点M关于点A的对称点S，点S关于点B的对称点为N，则$\overrightarrow{MN}$=（　　）

• A． $2（\overrightarrow b-\overrightarrow a）$
• B． $2（\overrightarrow a-\overrightarrow b）$
• C． $\frac{1}{2}（\overrightarrow b-\overrightarrow a）$
• D． $\frac{1}{2}（\overrightarrow a-\overrightarrow b）$

Answer 1

分析 根据点的对称关系，结合向量中点公式进行化简即可得到结论．

解答 解：∵M关于点A的对称点S，点S关于点B的对称点为N，
∴$\overrightarrow{OB}=\frac{1}{2}（\overrightarrow{ON}+\overrightarrow{OS}）$，$\overrightarrow{OA}=\frac{1}{2}（\overrightarrow{OM}+\overrightarrow{OS}）$．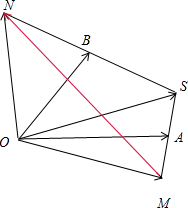
即$\overrightarrow{ON}$+$\overrightarrow{OS}$=2$\overrightarrow{OB}$=2$\overrightarrow b$，
$\overrightarrow{OM}$+$\overrightarrow{OS}$=2$\overrightarrow{OA}$=2$\overrightarrow a$，
两式相减得$\overrightarrow{ON}$-$\overrightarrow{OM}$=2$\overrightarrow b$-2$\overrightarrow a$
即$\overrightarrow{MN}$=$\overrightarrow{ON}$-$\overrightarrow{OM}$=2$\overrightarrow b$-2$\overrightarrow a$
=$2（\overrightarrow b-\overrightarrow a）$，
故选：A．

点评 本题考查了向量的运算和三角形法则，根据对称关系得到向量的中点公式是解决本题的关键．