题目内容
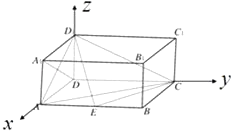
【题目】如图,在长方体ABCD﹣A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动. 
(1)证明:D1E⊥A1D;
(2)当E为AB的中点时,求点E到面ACD1的距离;
(3)AE等于何值时,二面角D1﹣EC﹣D的大小为 ![]() .
.
【答案】
(1)证明:分别以DA、DC、DD1为x、y、z轴,建立如图的坐标系,则 ![]() ,
,
设AE=x,则A1(1,0,1),D1(0,0,1),E(1,x,0),A(1,0,0),C(0,2,0).
则 ![]() =(1.x,﹣1),
=(1.x,﹣1), ![]() ,
,
∴D1E⊥A1D;
(2)解:当E为AB的中点时,E(1,1,0), ![]() ,
,
设平面ACD1的法向量是 ![]() ,
,
求出 ![]() ,
, ![]() ,
,
由 ![]() ,得
,得 ![]()
∵ ![]() =(1,1,﹣1)
=(1,1,﹣1)
由点到平面的距离公式,得 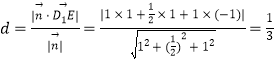 ,
,
∴点E到面ACD1的距离是 ![]() .
.
(3)解:设平面D1EC的法向量 ![]() =(a,b,c),
=(a,b,c),
∴ ![]() =(1,x﹣2,0),
=(1,x﹣2,0), ![]() =(0,2,﹣1),
=(0,2,﹣1), ![]() =(0,0,1).
=(0,0,1).
由 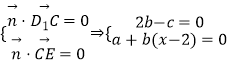 .
.
令b=1,
∴c=2,a=2﹣x.∴ ![]() =(2﹣x,1,2).
=(2﹣x,1,2).
依题意:cos ![]() =
= 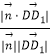 =
= ![]() ,
,
即 ![]() =
= ![]() ,
,
平方得(x﹣2)2= ![]() ,
,
∴ ![]() (不合题意,舍去),
(不合题意,舍去), ![]() .
.
∴ ![]() 时,二面角D1﹣EC﹣D的大小为
时,二面角D1﹣EC﹣D的大小为 ![]() .
.
【解析】(1)建立如图的坐标系,则 ![]() ,设E(1,t,0),则
,设E(1,t,0),则 ![]() ,通过向量的数量积为0,计算可得D1E⊥A1D;(2)当E为AB的中点时,E(1,1,0),
,通过向量的数量积为0,计算可得D1E⊥A1D;(2)当E为AB的中点时,E(1,1,0), ![]() ,求出平面ACD1的一个法向量,最后利用点到面的距离公式即可求点E到面ACD1的距离.(3)求出平面的法向量,利用二面角的夹角关系建立方程进行求解即可.
,求出平面ACD1的一个法向量,最后利用点到面的距离公式即可求点E到面ACD1的距离.(3)求出平面的法向量,利用二面角的夹角关系建立方程进行求解即可.

练习册系列答案
相关题目