题目内容
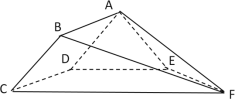
【题目】如图,梯形![]() 所在的平面与等腰梯形
所在的平面与等腰梯形![]() 所在的平面互相垂直,
所在的平面互相垂直,![]() ,
,![]() .
.![]() ,
,![]() .
.
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?不需说明理由.
?不需说明理由.

【答案】(1)详见解析(2)![]() (3)不存在
(3)不存在
【解析】
(1)根据平行四边形求得![]() ,再利用线面平行的判定定理得证;
,再利用线面平行的判定定理得证;
(2)建立空间直角坐标系![]() ,求出平面
,求出平面![]() 的法向量和平面
的法向量和平面![]() 的法向量,再利用夹角公式求得余弦值;
的法向量,再利用夹角公式求得余弦值;
(3)求得平面![]() 的法向量
的法向量![]() ,证明
,证明![]() 得出平面
得出平面![]() 与平面
与平面![]() 不可能垂直,得出不存在点G.
不可能垂直,得出不存在点G.
解:(1)因为![]() ,且
,且![]() ,所以四边形
,所以四边形![]() 为平行四边形,所以
为平行四边形,所以![]() .
.
因为![]() ,
,
所以![]() 平面
平面![]() .
.
(2)在平面ABEF内,过A作![]() ,因为平面
,因为平面![]()
![]() 平面
平面![]() ,
,
![]() ,
,![]() ,所以
,所以![]() ,
,
所以如图建立空间直角坐标系![]() .
.
由题意得,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
所以![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() 则
则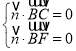 即
即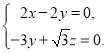
令![]() ,则
,则![]() ,
,![]() ,所以
,所以![]()
平面![]() 的一个法向量为
的一个法向量为![]()
则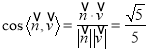 .所以二面角
.所以二面角![]() 的余弦值
的余弦值![]() .
.
(3)线段![]() 上不存在点
上不存在点![]() ,使得
,使得![]() 平面
平面![]() ,理由如下:
,理由如下:
解法一:设平面![]() 的法向量为
的法向量为![]()
![]() ,
,
则 即
即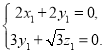
令![]() ,则
,则![]() ,
,![]() ,所以
,所以![]()
![]() .因为
.因为![]() ,
,
所以平面![]() 与平面
与平面![]() 不可能垂直,
不可能垂直,
从而线段![]() 上不存在点
上不存在点![]() ,使得
,使得![]() 平面
平面![]() .
.
解法二:线段![]() 上不存在点
上不存在点![]() ,使得
,使得![]() 平面
平面![]() ,理由如下:
,理由如下:
假设线段![]() 上存在点
上存在点![]() ,使得
,使得![]() 平面
平面![]() ,设
,设![]() ,其中
,其中![]() .
.
设![]() ,则有
,则有![]() ,
,
所以![]() ,
,![]() ,
,![]() ,从而
,从而![]() ,
,
所以![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() .所以有
.所以有![]() ,
,
因为上述方程组无解,所以假设不成立.
所以线段![]() 上不存在点
上不存在点![]() ,使得
,使得![]() 平面
平面![]() .
.

【题目】为了解某校学生参加社区服务的情况,采用按性别分层抽样的方法进行调查.已知该校共有学生960人,其中男生560人,从全校学生中抽取了容量为![]() 的样本,得到一周参加社区服务的时间的统计数据好下表:
的样本,得到一周参加社区服务的时间的统计数据好下表:
超过1小时 | 不超过1小时 | |
男 | 20 | 8 |
女 | 12 | m |
(Ⅰ)求![]() ,
,![]() ;
;
(Ⅱ)能否有95%的把握认为该校学生一周参加社区服务时间是否超过1小时与性别有关?
(Ⅲ)以样本中学生参加社区服务时间超过1小时的频率作为该事件发生的概率,现从该校学生中随机调查6名学生,试估计6名学生中一周参加社区服务时间超过1小时的人数.
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
![]()
【题目】苹果是人们日常生活中常见的营养型水果.某地水果批发市场销售来自5个不同产地的富士苹果,各产地的包装规格相同,它们的批发价格(元/箱)和市场份额如下:
产地 |
|
|
|
|
|
批发价格 |
|
|
|
|
|
市场份额 |
|
|
|
|
|
市场份额亦称“市场占有率”.指某一产品的销售量在市场同类产品中所占比重.
(1)从该地批发市场销售的富士苹果中随机抽取一箱,求该箱苹果价格低于![]() 元的概率;
元的概率;
(2)按市场份额进行分层抽样,随机抽取![]() 箱富士苹果进行检验,
箱富士苹果进行检验,
①从产地![]() 共抽取
共抽取![]() 箱,求
箱,求![]() 的值;
的值;
②从这![]() 箱苹果中随机抽取两箱进行等级检验,求两箱产地不同的概率;
箱苹果中随机抽取两箱进行等级检验,求两箱产地不同的概率;
(3)由于受种植规模和苹果品质的影响,预计明年产地![]() 的市场份额将增加
的市场份额将增加![]() ,产地
,产地![]() 的市场份额将减少
的市场份额将减少![]() ,其它产地的市场份额不变,苹果销售价格也不变(不考虑其它因素).设今年苹果的平均批发价为每箱
,其它产地的市场份额不变,苹果销售价格也不变(不考虑其它因素).设今年苹果的平均批发价为每箱![]() 元,明年苹果的平均批发价为每箱
元,明年苹果的平均批发价为每箱![]() 元,比较
元,比较![]() 的大小.(只需写出结论)
的大小.(只需写出结论)
【题目】据《人民网》报道,“美国国家航空航天局( NASA)发文称,相比20年前世界变得更绿色了.卫星资料显示中国和印度的行动主导了地球变绿.”据统计,中国新增绿化面积的42%来自于植树造林,下表是中国十个地区在2017年植树造林的相关数据.(造林总面积为人工造林、飞播造林、新封山育林、退化林修复、人工更新的面积之和)
单位:公顷
造林方式 | ||||||
地区 | 造林总面积 | 人工造林 | 飞播造林 | 新封山育林 | 退化林修复 | 人工更新 |
内蒙 | 618484 | 311052 | 74094 | 136006 | 90382 | 6950 |
河北 | 583361 | 345625 | 33333 | 135107 | 65653 | 3643 |
河南 | 149002 | 97647 | 13429 | 22417 | 15376 | 133 |
重庆 | 226333 | 100600 | 62400 | 63333 | ||
陕西 | 297642 | 33602 | 63865 | 16067 | ||
甘肃 | 325580 | 260144 | 57438 | 7998 | ||
新疆 | 263903 | 118105 | 6264 | 126647 | 10796 | 2091 |
青海 | 178414 | 16051 | 159734 | 2629 | ||
宁夏 | 91531 | 58960 | 22938 | 8298 | 1335 | |
北京 | 19064 | 10012 | 4000 | 3999 | 1053 | |
(I)请根据上述数据分别写出在这十个地区中人工造林面积与造林总面积的比值最大和最小的地区;
(Ⅱ)在这十个地区中,任选一个地区,求该地区人工造林面积占造林总面积的比值超过![]() 的概率是多少?
的概率是多少?
(Ⅲ)在这十个地区中,从新封山育林面积超过五万公顷的地区中,任选两个地区,记X为这两个地区中退化林修复面积超过六万公顷的地区的个数,求X的分布列及数学期望.