��Ŀ����
5�����������ĸ����⣺��1����0������$\frac{��}{2}$ʱ��sin��������tan����
��2�����У�����$\frac{3��}{2}$ʱ��sin��+cos����-1��
��3����֪A={x|x=n��+��-1��n$\frac{��}{2}$��n��Z}��B={x|x=2k��+$\frac{��}{2}$��k��Z}����A=B��
��4�����ABC����tanA+tanB+tanC=tanAtanBtanC��
���ں��������������ȷ�������ţ�1����2����3����4����
���� �������Ǻ����߿��жϣ�1�������������ͺ�����ͼ������ʣ����жϣ�2�����������߽ǵı�ʾ���������жϣ�3�����������Ǻ͵����й�ʽ�����жϣ�4����
��� �⣺��ֱ������ϵ�н�ϵ�λԲ������Ǧ��������ߺ������ߣ�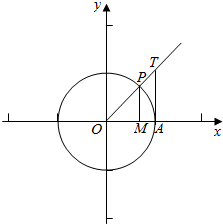
��ͼ��֪sin��=MP����=$\widehat{AP}$��tan��=AT��
��S��AOP=$\frac{1}{2}$��MP��1=$\frac{1}{2}$sin����S����AOP=$\frac{1}{2}$��$\widehat{AP}$��1=$\frac{1}{2}$����S��AOT=$\frac{1}{2}$��AT��1=$\frac{1}{2}$tan����S��AOP��S����AOP��S��AOT��
��MP��$\widehat{AP}$��AT����sin��������tan����
�ʣ�1����ȷ��
sin��+cos��=$\sqrt{2}$sin����+$\frac{��}{4}$����
�ߦУ�����$\frac{3��}{2}$��
��$\frac{5��}{4}$����+$\frac{��}{4}$��$\frac{7��}{4}$��
��$-\sqrt{2}$��$\sqrt{2}$sin����+$\frac{��}{4}$����-1��
�ʣ�2����ȷ��
��A={x|x=n��+��-1��n$\frac{��}{2}$��n��Z}��ʾ�ձ�����y��Ǹ������ϵĽǣ�
B={x|x=2k��+$\frac{��}{2}$��k��Z}Ҳ��ʾ�ձ�����y��Ǹ������ϵĽǣ�
��A=B��
��4�����ABC��
tanA+tanB+tanC=tanA+tanB-tan��A+B��=tanA+tanB-$\frac{tanA+tanB}{1-tanA•tanB}$=��tanA+tanB����1-$\frac{1}{1-tanA•tanB}$��=��tanA+tanB��$\frac{-tanA•tanB}{1-tanA•tanB}$=$\frac{tanA+tanB}{1-tanA•tanB}$•tanAtanB=tanAtanBtanC��
�ʣ�4����ȷ��
����ȷ��������Ϊ����1����2����3����4����
�ʴ�Ϊ����1����2����3����4��
���� ���������������ж�Ϊ���壬���������Ǻ����ߣ����Ǻ�����ͼ������ʣ����߽ǣ����Ǻ�ȱ任��֪ʶ�㣬�Ѷ��е���

 ��ڽ��ȫ������ϵ�д�
��ڽ��ȫ������ϵ�д�| A�� | 2$\sqrt{2}$R3 | B�� | $\frac{4}{3}$��R3 | C�� | $\frac{8}{9}$$\sqrt{3}$R3 | D�� | $\frac{\sqrt{3}}{9}$R3 |
| A�� | �Ȳ����� | B�� | �ȱ����� | ||
| C�� | ���ǵȲ����У����ǵȱ����� | D�� | ���϶�����ȷ |
| ���� �Ա� | ��ͬ | ���� | �ϼ� |
| �� | 198 | 217 | 415 |
| Ů | 476 | 107 | 585 |
| �ϼ� | 674 | 326 | 1000 |
����K2=$\frac{n��ad-bc��^{2}}{��a+b����c+d����a+c����b+d��}$��
| ��P��K2��k�� | ��0.10 | ��0.05 | 0.025�� | ��0.010 | ��0.005 | ��0.001 |
| ��k | ��2.760 | ��3.841 | ��5.024 | ��60635 | 7.879�� | ��10.828 |
| ��������x��cm�� | 176 | 173 | 179 |
| ��������y��cm�� | 173 | 179 | 185 |
������һ������������ʽ1����$\stackrel{��}{b}$����������ʽ3������$\stackrel{��}{a}$��������ع�ֱ�߷��̣�
��������������������ʽ2����$\stackrel{��}{b}$����������ʽ3����$\stackrel{��}{a}$��������ع�ֱ�߷��̣�
��������������X=x-173��Y=y-179����һ��ת��������ģ���������
| X | 3 | 0 | 6 |
| Y | -6 | 0 | 6 |
��������ص���ѡһ�ַ�������y��x�Ļع鷽��$\stackrel{��}{y}$=$\stackrel{��}{b}$x+$\stackrel{��}{a}$�������ݻع�ֱ��Ԥ����ѧ��ʦ�����ӵ����ߣ�
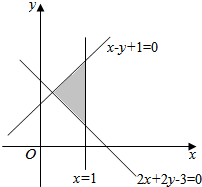 ��x��y�����Լ��������������������ͼ����Ӱ���֣����߽磩��ʾ����Ŀ�꺯��z=3x-y�����ֵ��$\frac{5}{2}$��
��x��y�����Լ��������������������ͼ����Ӱ���֣����߽磩��ʾ����Ŀ�꺯��z=3x-y�����ֵ��$\frac{5}{2}$��