题目内容
10．设函数f（x）=x3（ax+m•a-x）（x∈R，a＞0）且a≠1）是偶函数，则实数m的值为（ ）| A． | -2 | B． | -1 | C． | 1 | D． | 2 |
分析 根据函数奇偶性的性质，结合函数f（x）=x3（ax+m•a-x）为偶函数，可得：函数g（x）=ax+m•a-x为奇函数，根据g（0）=0，可得答案．
解答 解：∵函数f（x）=x3（ax+m•a-x）为偶函数，
∴函数g（x）=ax+m•a-x为奇函数，
∴g（0）=1+m=0，
∴m=-1，
故选：B
点评 本题考查的知识点是函数奇偶性的性质，熟练掌握函数奇偶性的性质，是解答的关键．
练习册系列答案
点睛新教材全能解读系列答案
小学教材完全解读系列答案
相关题目
18．某企业产品的成本前两年递增20%，经过引进的技术设备，并实施科学管理，后两年的产品成本每年递减20%，那么该企业产品的成本现在与原来比较（ ）
| A． | 不增不减 | B． | 增多了 | ||
| C． | 减少了 | D． | 以原来的成本大小有关 |
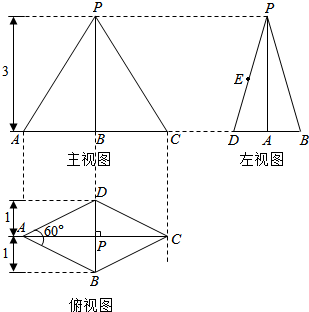一个四棱锥的三视图和直观图如图所示，E为侧棱PD的中点．