题目内容
20．
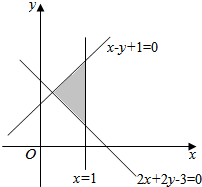由x，y满足的约束条件，作出可行域如图中阴影部分（含边界）所示，则目标函数z=3x-y的最大值是$\frac{5}{2}$．
分析 化目标函数为直线方程的斜截式，数形结合得到最优解，联立方程组求得最优解的坐标，代入目标函数得答案．
解答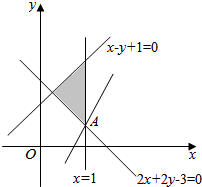 
解：联立$\left\{\begin{array}{l}{x=1}\\{2x+2y-3=0}\end{array}\right.$，解得：A（1，$\frac{1}{2}$）．
化目标函数z=3x-y为y=3x-z，
由图可知，当直线y=3x-z过A点时，直线在y轴上的截距最小，z有最大值为：3×$1-\frac{1}{2}=\frac{5}{2}$．
故答案为：$\frac{5}{2}$．
点评 本题考查简单的线性规划，考查了数形结合的解题思想方法，是中档题．
练习册系列答案
相关题目
8．若g（x）=1-2x，f[g（x）]=$\frac{1-x}{1+x}$，则f（4）=（ ）
| A． | -5 | B． | 5 | C． | -10 | D． | 10 |
15．已知a＞b，则下面结论正确的是（ ）
| A． | $\frac{1}{a}＜\frac{1}{b}$ | B． | $\frac{a}{b}＞1$ | C． | |a|＞b | D． | ac2＞bc2 |
12．已知f（x）是定义在实数集R上的可导函数，且其导函数为f′（x），若f′（x）＜f（x）在R上恒成立，则不等式ef（x）＞f（1）ex上的解集为（ ）
| A． | （1，+∞） | B． | （-∞，1） | C． | （-1，1） | D． | （-∞，1）∪（1，+∞） |
9．已知$f（x+\frac{1}{x}）={x^2}+\frac{1}{x^2}$，则函数f（x）=（ ）
| A． | x2-2（x≠0） | B． | x2-2（x≥2） | C． | x2-2（|x|≥2） | D． | x2-2 |
10．若函数f（x）=$\frac{x+b}{（2x+1）（x-a）}$为奇函数，则a+b=（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{2}{3}$ | C． | $\frac{3}{4}$ | D． | 1 |