题目内容
已知椭圆的中心在坐标原点O,焦点在x轴上,短轴长为2,且两个焦点和短轴的两个端点恰为一个正方形的顶点.过右焦点F与x轴不垂直的直线l交椭圆于P,Q两点.(1)求椭圆的方程;
(2)当直线l的斜率为1时,求△POQ的面积;
(3)在线段OF上是否存在点M(m,0),使得以MP,MQ为邻边的平行四边形是菱形?若存在,求出m的取值范围;若不存在,请说明理由.
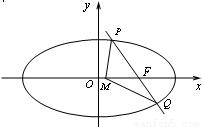
【答案】分析:(1)设椭圆方程为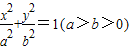 .由两个焦点和短轴的两个端点恰为正方形的顶点,且短轴长为2,由此能够求出a,b,c的值,从而得到所求椭圆方程.
.由两个焦点和短轴的两个端点恰为正方形的顶点,且短轴长为2,由此能够求出a,b,c的值,从而得到所求椭圆方程.
(2)右焦点F(1,0),直线l的方程为y=x-1.设P(x1,y1),Q(x2,y2),由题设条件得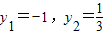 .由此入手可求出
.由此入手可求出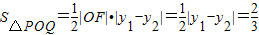 .
.
(3)假设在线段OF上存在点M(m,0)(0<m<1),使得以MP,MQ为邻边的平行四边形是菱形.因为直线与x轴不垂直,设直线l的方程为y=k(x-1)(k≠0).由题意知(1+2k2)x2-4k2x+2k2-2=0.由此可知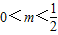 .
.
解答:解:(1)由已知,椭圆方程可设为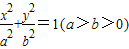 .(1分)
.(1分)
∵两个焦点和短轴的两个端点恰为正方形的顶点,且短轴长为2,
∴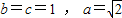 .
.
所求椭圆方程为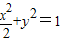 .(4分)
.(4分)
(2)右焦点F(1,0),直线l的方程为y=x-1.
设P(x1,y1),Q(x2,y2),
由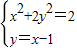 得3y2+2y-1=0,解得
得3y2+2y-1=0,解得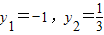 .
.
∴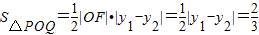 .(9分)
.(9分)
(3)假设在线段OF上存在点M(m,0)(0<m<1),使得以MP,MQ为邻边的平行四边形是菱形.因为直线与x轴不垂直,所以设直线l的方程为y=k(x-1)(k≠0).
由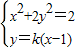 可得(1+2k2)x2-4k2x+2k2-2=0.
可得(1+2k2)x2-4k2x+2k2-2=0.
∴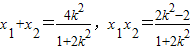 .
.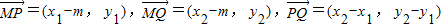 .其中x2-x1≠0
.其中x2-x1≠0
以MP,MQ为邻边的平行四边形是菱形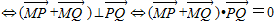 ?(x1+x2-2m,y1+y2)(x2-x1,y2-y1)=0?(x1+x2-2m)(x2-x1)+(y1+y2)(y2-y1)=0?(x1+x2-2m)+k(y1+y2)=0
?(x1+x2-2m,y1+y2)(x2-x1,y2-y1)=0?(x1+x2-2m)(x2-x1)+(y1+y2)(y2-y1)=0?(x1+x2-2m)+k(y1+y2)=0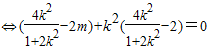 ?2k2-(2+4k2)m=0
?2k2-(2+4k2)m=0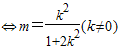 .
.
∴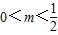 .(14分)
.(14分)
点评:本题考查圆锥曲线的位置关系,解题时要认真审题,仔细解答.
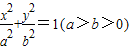 .由两个焦点和短轴的两个端点恰为正方形的顶点,且短轴长为2,由此能够求出a,b,c的值,从而得到所求椭圆方程.
.由两个焦点和短轴的两个端点恰为正方形的顶点,且短轴长为2,由此能够求出a,b,c的值,从而得到所求椭圆方程.(2)右焦点F(1,0),直线l的方程为y=x-1.设P(x1,y1),Q(x2,y2),由题设条件得
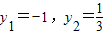 .由此入手可求出
.由此入手可求出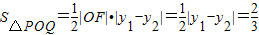 .
.(3)假设在线段OF上存在点M(m,0)(0<m<1),使得以MP,MQ为邻边的平行四边形是菱形.因为直线与x轴不垂直,设直线l的方程为y=k(x-1)(k≠0).由题意知(1+2k2)x2-4k2x+2k2-2=0.由此可知
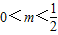 .
.解答:解:(1)由已知,椭圆方程可设为
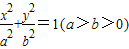 .(1分)
.(1分)∵两个焦点和短轴的两个端点恰为正方形的顶点,且短轴长为2,
∴
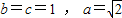 .
.所求椭圆方程为
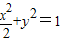 .(4分)
.(4分)(2)右焦点F(1,0),直线l的方程为y=x-1.
设P(x1,y1),Q(x2,y2),
由
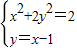 得3y2+2y-1=0,解得
得3y2+2y-1=0,解得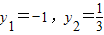 .
.∴
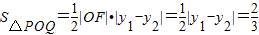 .(9分)
.(9分)(3)假设在线段OF上存在点M(m,0)(0<m<1),使得以MP,MQ为邻边的平行四边形是菱形.因为直线与x轴不垂直,所以设直线l的方程为y=k(x-1)(k≠0).
由
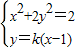 可得(1+2k2)x2-4k2x+2k2-2=0.
可得(1+2k2)x2-4k2x+2k2-2=0.∴
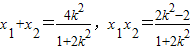 .
.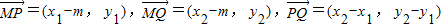 .其中x2-x1≠0
.其中x2-x1≠0以MP,MQ为邻边的平行四边形是菱形
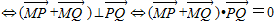 ?(x1+x2-2m,y1+y2)(x2-x1,y2-y1)=0?(x1+x2-2m)(x2-x1)+(y1+y2)(y2-y1)=0?(x1+x2-2m)+k(y1+y2)=0
?(x1+x2-2m,y1+y2)(x2-x1,y2-y1)=0?(x1+x2-2m)(x2-x1)+(y1+y2)(y2-y1)=0?(x1+x2-2m)+k(y1+y2)=0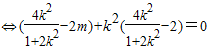 ?2k2-(2+4k2)m=0
?2k2-(2+4k2)m=0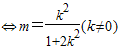 .
.∴
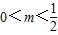 .(14分)
.(14分)点评:本题考查圆锥曲线的位置关系,解题时要认真审题,仔细解答.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
 已知椭圆的中心在坐标原点O,焦点在x轴上,短轴长为2,且两个焦点和短轴的两个端点恰为一个正方形的顶点.过右焦点F与x轴不垂直的直线l交椭圆于P,Q两点.
已知椭圆的中心在坐标原点O,焦点在x轴上,短轴长为2,且两个焦点和短轴的两个端点恰为一个正方形的顶点.过右焦点F与x轴不垂直的直线l交椭圆于P,Q两点.