题目内容
已知函数 ,a∈R.
,a∈R.(1)当a=1时,求函数f(x)的最大值;
(2)如果对于区间
 上的任意一个x,都有f(x)≤1成立,求a的取值范围.
上的任意一个x,都有f(x)≤1成立,求a的取值范围.
【答案】分析:(1)结合函数解析式的结构特征对函数进行配方可得 ,进而得到函数的最大值.
,进而得到函数的最大值.
(2)根据函数解析式的特征对函数进行配方可得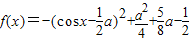 ,结合函数的定义域进行换元可得二次函数,即可利用二次函数的性质求出函数的最值,进而解决恒成立问题.
,结合函数的定义域进行换元可得二次函数,即可利用二次函数的性质求出函数的最值,进而解决恒成立问题.
解答:解:(1)由题意可得: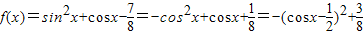 .
.
所以当 时,函数f(x)的最大值是
时,函数f(x)的最大值是 .
.
(2)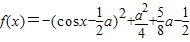 .
.
当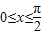 时,0≤cosx≤1,令t=cosx,则0≤t≤1.
时,0≤cosx≤1,令t=cosx,则0≤t≤1.
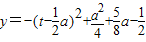 ,0≤t≤1.
,0≤t≤1.
当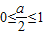 ,即0≤a≤2时,则当
,即0≤a≤2时,则当 ,即
,即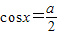 时,
时,
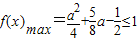 ,
,
解得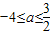 ,
,
则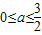 ;
;
当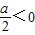 ,即a<0时,则当t=0即cosx=0时,
,即a<0时,则当t=0即cosx=0时,
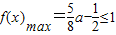 ,
,
解得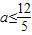 ,
,
则a<0.
当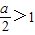 ,即a>2时,则当t=1即cosx=1时,
,即a>2时,则当t=1即cosx=1时,
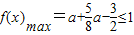 ,
,
解得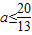 ,无解.
,无解.
综上可知,a的取值范围 .
.
点评:解决此类问题的关键是熟练掌握二次函数的有关性质,二次函数的对称轴与区间的位置关系可以确定函数的最值.
 ,进而得到函数的最大值.
,进而得到函数的最大值.(2)根据函数解析式的特征对函数进行配方可得
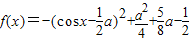 ,结合函数的定义域进行换元可得二次函数,即可利用二次函数的性质求出函数的最值,进而解决恒成立问题.
,结合函数的定义域进行换元可得二次函数,即可利用二次函数的性质求出函数的最值,进而解决恒成立问题.解答:解:(1)由题意可得:
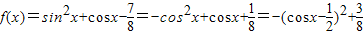 .
.所以当
 时,函数f(x)的最大值是
时,函数f(x)的最大值是 .
.(2)
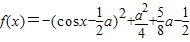 .
.当
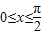 时,0≤cosx≤1,令t=cosx,则0≤t≤1.
时,0≤cosx≤1,令t=cosx,则0≤t≤1.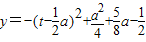 ,0≤t≤1.
,0≤t≤1.当
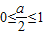 ,即0≤a≤2时,则当
,即0≤a≤2时,则当 ,即
,即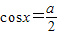 时,
时,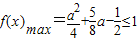 ,
,解得
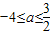 ,
,则
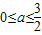 ;
; 当
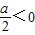 ,即a<0时,则当t=0即cosx=0时,
,即a<0时,则当t=0即cosx=0时,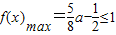 ,
,解得
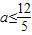 ,
,则a<0.
当
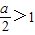 ,即a>2时,则当t=1即cosx=1时,
,即a>2时,则当t=1即cosx=1时,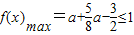 ,
,解得
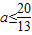 ,无解.
,无解.综上可知,a的取值范围
 .
.点评:解决此类问题的关键是熟练掌握二次函数的有关性质,二次函数的对称轴与区间的位置关系可以确定函数的最值.

练习册系列答案
相关题目
 (a∈R且a≠0).
(a∈R且a≠0).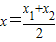 ;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”.
;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”. (a∈R且a≠0).
(a∈R且a≠0). ;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”.
;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”. (a∈R且a≠0).
(a∈R且a≠0). ;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”.
;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”. (a∈R).
(a∈R). 在[1,e]上是增函数,求a的取值范围;
在[1,e]上是增函数,求a的取值范围;
 .
.