题目内容
已知函数 (a∈R且a≠0).
(a∈R且a≠0).(Ⅰ)求函数f(x)的单调区间;
(Ⅱ) 记函数y=F(x)的图象为曲线C.设点A(x1,y1),B(x2,y2)是曲线C上的不同两点,如果在曲线C上存在点M(x,y),使得:①
 ;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”.
;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”.试问:函数f(x)是否存在“中值相依切线”,请说明理由.
【答案】分析:(I)根据对数函数的定义求得函数的定义域,再根据f(x)的解析式求出f(x)的导函数,然后分别令导函数大于0和小于0得到关于x的不等式,求出不等式的解集即可得到相应的x的范围即分别为函数的递增和递减区间;
(II)假设函数f(x)的图象上存在两点A(x1,y1),B(x2,y2),使得AB存在“中值相依切线”,根据斜率公式求出直线AB的斜率,利用导数的几何意义求出直线AB的斜率,它们相等,再通过构造函数,利用导数研究函数的单调性和最值即可证明结论.
解答:解:(Ⅰ)函数f(x)的定义域是(0,+∞).…(1分)
由已知得,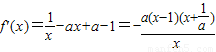 .…(2分)
.…(2分)
(1)当a>0时,令f'(x)>0,解得0<x<1; 令f'(x)<0,解得x>1.
所以函数f(x)在(0,1)上单调递增,在(1,+∞)上单调递减.…(3分)
(2)当a<0时,
①当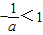 时,即a<-1时,令f'(x)>0,解得
时,即a<-1时,令f'(x)>0,解得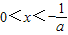 或x>1;
或x>1;
令f'(x)<0,解得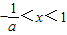 .
.
所以,函数f(x)在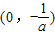 和(1,+∞)上单调递增,在
和(1,+∞)上单调递增,在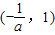 上单调递减;…(4分)
上单调递减;…(4分)
②当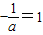 时,即a=-1时,显然,函数f(x)在(0,+∞)上单调递增; …(5分)
时,即a=-1时,显然,函数f(x)在(0,+∞)上单调递增; …(5分)
③当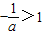 时,即-1<a<0时,令f'(x)>0,解得0<x<1或
时,即-1<a<0时,令f'(x)>0,解得0<x<1或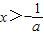 ;
;
令f'(x)<0,解得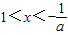 .
.
所以,函数f(x)在(0,1)和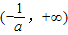 上单调递增,在
上单调递增,在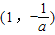 上单调递减.…(6分)
上单调递减.…(6分)
综上所述,(1)当a>0时,函数f(x)在(0,1)上单调递增,在(1,+∞)上单调递减;
(2)当a<-1时,函数f(x)在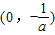 和(1,+∞)上单调递增,在
和(1,+∞)上单调递增,在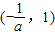 上单调递减;
上单调递减;
(3)当a=-1时,函数f(x)在(0,+∞)上单调递增;
(4)当-1<a<0时,函数f(x)在(0,1)和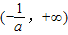 上单调递增,在
上单调递增,在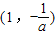 上单调递减.…(7分)
上单调递减.…(7分)
(Ⅱ)假设函数f(x)存在“中值相依切线”.
设A(x1,y1),B(x2,y2)是曲线y=f(x)上的不同两点,且0<x1<x2,
则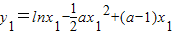 ,
,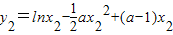 .
.
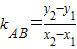 =
=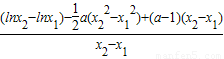
=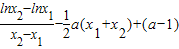 …(8分)
…(8分)
曲线在点M(x,y)处的切线斜率k=f'(x)=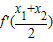 =
=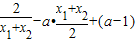 ,…(9分)
,…(9分)
依题意得: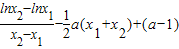 =
=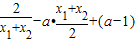 .
.
化简可得: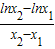 =
=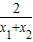 ,
,
即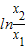 =
=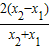 =
=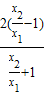 .…(11分)
.…(11分)
设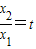 (t>1),上式化为:
(t>1),上式化为: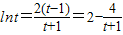 ,
,
即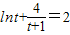 .…(12分)
.…(12分)
令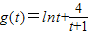 ,
,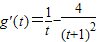 =
=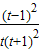 .
.
因为t>1,显然g'(t)>0,所以g(t)在(1,+∞)上递增,
显然有g(t)>2恒成立.
所以在(1,+∞)内不存在t,使得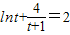 成立.
成立.
综上所述,假设不成立.所以,函数f(x)不存在“中值相依切线”.…(14分)
点评:此题考查学生会利用导函数的正负求出函数的单调区间,灵活运用中点坐标公式化简求值,掌握反证法进行命题证明的方法,是一道综合题,属难题.
(II)假设函数f(x)的图象上存在两点A(x1,y1),B(x2,y2),使得AB存在“中值相依切线”,根据斜率公式求出直线AB的斜率,利用导数的几何意义求出直线AB的斜率,它们相等,再通过构造函数,利用导数研究函数的单调性和最值即可证明结论.
解答:解:(Ⅰ)函数f(x)的定义域是(0,+∞).…(1分)
由已知得,
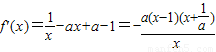 .…(2分)
.…(2分)(1)当a>0时,令f'(x)>0,解得0<x<1; 令f'(x)<0,解得x>1.
所以函数f(x)在(0,1)上单调递增,在(1,+∞)上单调递减.…(3分)
(2)当a<0时,
①当
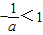 时,即a<-1时,令f'(x)>0,解得
时,即a<-1时,令f'(x)>0,解得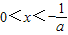 或x>1;
或x>1;令f'(x)<0,解得
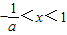 .
.所以,函数f(x)在
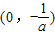 和(1,+∞)上单调递增,在
和(1,+∞)上单调递增,在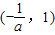 上单调递减;…(4分)
上单调递减;…(4分)②当
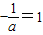 时,即a=-1时,显然,函数f(x)在(0,+∞)上单调递增; …(5分)
时,即a=-1时,显然,函数f(x)在(0,+∞)上单调递增; …(5分)③当
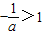 时,即-1<a<0时,令f'(x)>0,解得0<x<1或
时,即-1<a<0时,令f'(x)>0,解得0<x<1或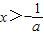 ;
;令f'(x)<0,解得
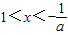 .
.所以,函数f(x)在(0,1)和
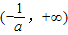 上单调递增,在
上单调递增,在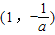 上单调递减.…(6分)
上单调递减.…(6分)综上所述,(1)当a>0时,函数f(x)在(0,1)上单调递增,在(1,+∞)上单调递减;
(2)当a<-1时,函数f(x)在
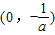 和(1,+∞)上单调递增,在
和(1,+∞)上单调递增,在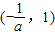 上单调递减;
上单调递减;(3)当a=-1时,函数f(x)在(0,+∞)上单调递增;
(4)当-1<a<0时,函数f(x)在(0,1)和
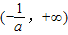 上单调递增,在
上单调递增,在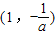 上单调递减.…(7分)
上单调递减.…(7分) (Ⅱ)假设函数f(x)存在“中值相依切线”.
设A(x1,y1),B(x2,y2)是曲线y=f(x)上的不同两点,且0<x1<x2,
则
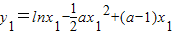 ,
,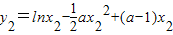 .
.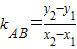 =
=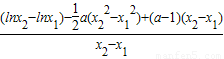
=
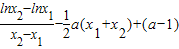 …(8分)
…(8分)曲线在点M(x,y)处的切线斜率k=f'(x)=
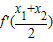 =
=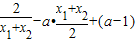 ,…(9分)
,…(9分)依题意得:
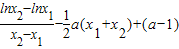 =
=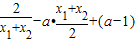 .
.化简可得:
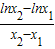 =
=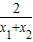 ,
,即
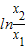 =
=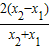 =
=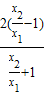 .…(11分)
.…(11分)设
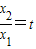 (t>1),上式化为:
(t>1),上式化为: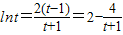 ,
,即
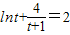 .…(12分)
.…(12分)令
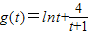 ,
,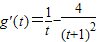 =
=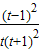 .
.因为t>1,显然g'(t)>0,所以g(t)在(1,+∞)上递增,
显然有g(t)>2恒成立.
所以在(1,+∞)内不存在t,使得
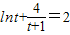 成立.
成立.综上所述,假设不成立.所以,函数f(x)不存在“中值相依切线”.…(14分)
点评:此题考查学生会利用导函数的正负求出函数的单调区间,灵活运用中点坐标公式化简求值,掌握反证法进行命题证明的方法,是一道综合题,属难题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (a∈R且a≠0).
(a∈R且a≠0). ;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”.
;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”.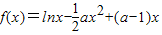 (a∈R且a≠0).
(a∈R且a≠0).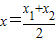 ;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”.
;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”.