题目内容
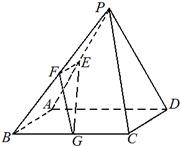
已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E、F、G分别是PA、PB、BC的中点.
(1)求证:EF⊥平面PAD;
(2)求平面EFG与平面ABCD所成锐二面角的大小;
(3)若M为线段AB上靠近A的一个动点,问当AM长度等于多少时,直线MF与平面EFG所成角的正弦值等于
?
分析:方法一(1)由面面垂直来证线面垂直,本题中先证明AB⊥平面PAD,再由EF∥AB得出EF⊥平面PAD;
(2)建立空间坐标系,分别求出两平面的法向量用相关公式求出两个平面的夹角的余弦值,再求出角的大小;
(3)设AM=x,给出相应的坐标,求出向量MF的坐标,利用线面角的相关公式求出线面角;
方法二 在(1)的证明中用了向量,其它基本与方法一同;
方法三 完全用几何法解决问题(1)中用的是线面平行的判定定理;
(2)根据几何性质作出二面角的平面角,再证明,求之;
(3)作出线面角,根据正弦值等于
建立关于参数的方程,求出参数值.
解答:解:
方法1:(1)证明:∵平面PAD⊥平面ABCD,AB⊥AD,
∴AB⊥平面PAD,(2分)
∵E、F为PA、PB的中点,
∴EF∥AB,∴EF⊥平面PAD;(4分)
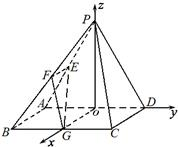
(2)解:过P作AD的垂线,垂足为O,
∵平面PAD⊥平面ABCD,则PO⊥平面ABCD.
连OG,以OG,OD,OP为x、y、z轴建立空间坐标系,(6分)
∵PA=PD=AD=4,
∴
OP=2,OD=OA=2,
得
A(0,-2,0),B(4,-2,0),C(4,2,0),D(0,2,0),P(0,0,2),
E(0,-1,),F(2,-1,),G(4,0,0),
故
=(2,0,0),=(4,1,-),
设平面EFG的一个法向量为n=(x,y,z)
则
,即取z=1,得n=(0,,1)(7分)
平面ABCD的一个法向量为,n
1=(0,0,1)
平面EFG与平面ABCD所成锐二面角的余弦值是:
|cos<n,n1>=||=,
锐二面角的大小是60°(8分)
(3)设AM=x,M(x,-2,0),则
=(2-x,1,),
设MF与平面EFG所成角为θ,
则
sinθ=|cos<n,>=||==,x=1或x=3,
∵M靠近A,∴x=1(10分)
∴当AM=1时,MF与平面EFG所成角正弦值等于
.(12分)
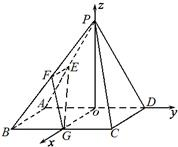
方法2:(1)证明:过P作PO⊥AD于O,∵平面PAD⊥平面ABCD,
则PO⊥平面ABCD,连OG,以OG,OD,OP为x、y、z轴建立空间坐标系,
(2分)
∵PA=PD=AD=4,∴
OP=2,OD=OA=2,
得
A(0,-2,0),B(4,-2,0),C(4,2,0),D(0,2,0),P(0,0,2),
E(0,-1,),F(2,-1,),G(4,0,0),
故
=(2,0,0),=(0,4,0),=(0,2,-2),
∵
•=0,•=0,
∴EF⊥平面PAD;(4分)
(2)解:
=(2,0,0),=(4,1,-),
设平面EFG的一个法向量为n=(x,y,z),
则
,即取z=1,得n=(0,,1)(7分)
平面ABCD的一个法向量为n
1=(0,0,1),以下同方法1
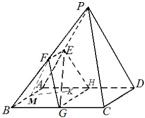
方法3:(I)证明:∵平面PAD⊥平面ABCD,AB⊥AD,
∴AB⊥平面PAD,(2分)
∵E、F为PA、PB的中点,
∴EF∥AB,∴EF⊥平面PAD;(4分)
(2)解:∵EF∥HG,AB∥HG,∴HG是所二面角的棱,(6分)
∵HG∥EF,∴HG⊥平面PAD,∴DH⊥HG,EH⊥HG,
∴∠EHA是锐二面角的平面角,等于60°;(8分)
(3)解:过M作MK⊥平面EFG于K,连接KF,
则∠KFM即为MF与平面EFG所成角,(10分)
因为AB∥EF,故AB∥平面EFG,故AB的点M到平面EFG的距离等于A到平面EFG的距离,
∵HG⊥平面PAD,∴平面EFGH⊥平面PBD于EH,
∴A到平面EFG的距离即三角形EHA的高,等于
,即MK=
,
∴
=,
FM=,在直角梯形EFMA中,AE=EF=2,
∴AM=1或AM=3∵M靠近A,∴AM=1(11分)
∴当AM=1时,MF与平面EFG所成角正弦值等于
.(12分)
点评:立体几何中点线面的关系问题的解决中常用的方法有三,一是用立体几何的方法,二是用空间向量法,三是立体几何与向量二者结合的方法.
练习册系列答案
相关题目
 已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E、F、G分别是PA、PB、BC的中点.
已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E、F、G分别是PA、PB、BC的中点. (2)解:过P作AD的垂线,垂足为O,
(2)解:过P作AD的垂线,垂足为O, 方法2:(1)证明:过P作PO⊥AD于O,∵平面PAD⊥平面ABCD,
方法2:(1)证明:过P作PO⊥AD于O,∵平面PAD⊥平面ABCD, 方法3:(I)证明:∵平面PAD⊥平面ABCD,AB⊥AD,
方法3:(I)证明:∵平面PAD⊥平面ABCD,AB⊥AD, (2)解:过P作AD的垂线,垂足为O,
(2)解:过P作AD的垂线,垂足为O, 方法2:(1)证明:过P作PO⊥AD于O,∵平面PAD⊥平面ABCD,
方法2:(1)证明:过P作PO⊥AD于O,∵平面PAD⊥平面ABCD, 方法3:(I)证明:∵平面PAD⊥平面ABCD,AB⊥AD,
方法3:(I)证明:∵平面PAD⊥平面ABCD,AB⊥AD,
 一本好题口算题卡系列答案
一本好题口算题卡系列答案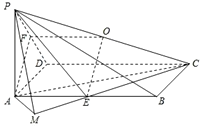 已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E、F分别是AB、PD的中点.
已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E、F分别是AB、PD的中点. (2012•即墨市模拟)已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2a,AB=a,PA⊥平米ABCD,F是线段BC的中点.H为PD中点.
(2012•即墨市模拟)已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2a,AB=a,PA⊥平米ABCD,F是线段BC的中点.H为PD中点. (2012•即墨市模拟)已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2a,AB=a,PA⊥平米ABCD,F是线段BC的中点.H为PD中点.
(2012•即墨市模拟)已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2a,AB=a,PA⊥平米ABCD,F是线段BC的中点.H为PD中点. 如图,已知在四棱锥P-ABCD中,底面ABCD是菱形,PA⊥底面ABCD,AB=1,PA•AC=1,∠ABC=θ(0<θ<
如图,已知在四棱锥P-ABCD中,底面ABCD是菱形,PA⊥底面ABCD,AB=1,PA•AC=1,∠ABC=θ(0<θ< (2012•枣庄二模)已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.
(2012•枣庄二模)已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.