题目内容
如图,互相垂直的两条公路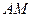 、
、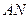 旁有一矩形花园
旁有一矩形花园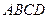 ,现欲将其扩建成一个更大的三角形花园
,现欲将其扩建成一个更大的三角形花园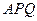 ,要求
,要求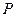 在射线
在射线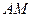 上,
上,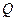 在射线
在射线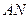 上,且
上,且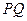 过点
过点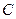 ,其中
,其中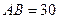 米,
米,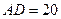 米. 记三角形花园
米. 记三角形花园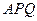 的面积为S.
的面积为S.
(Ⅰ)当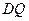 的长度是多少时,S最小?并求S的最小值.
的长度是多少时,S最小?并求S的最小值.
(Ⅱ)要使S不小于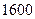 平方米,则
平方米,则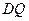 的长应在什么范围内?
的长应在什么范围内?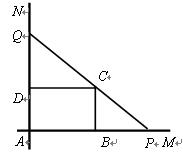
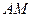 、
、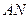 旁有一矩形花园
旁有一矩形花园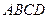 ,现欲将其扩建成一个更大的三角形花园
,现欲将其扩建成一个更大的三角形花园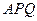 ,要求
,要求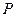 在射线
在射线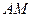 上,
上,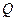 在射线
在射线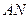 上,且
上,且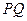 过点
过点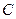 ,其中
,其中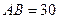 米,
米,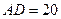 米. 记三角形花园
米. 记三角形花园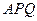 的面积为S.
的面积为S.(Ⅰ)当
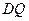 的长度是多少时,S最小?并求S的最小值.
的长度是多少时,S最小?并求S的最小值.(Ⅱ)要使S不小于
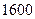 平方米,则
平方米,则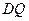 的长应在什么范围内?
的长应在什么范围内?
(Ⅰ)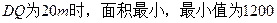
(Ⅱ)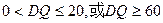
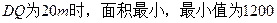
(Ⅱ)
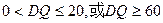
(Ⅰ)设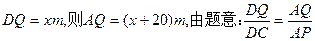 ,
,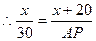 ,
,
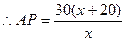 ………… 2分
………… 2分
则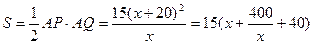
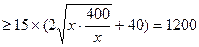 ………… 4分
………… 4分
当且仅当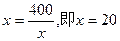 时等号成立………… 5分
时等号成立………… 5分
(Ⅱ)由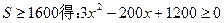 ………… 7分
………… 7分
解得: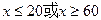
又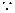
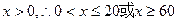 ………… 9分
………… 9分
答:(1)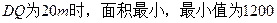 ;
;
(2)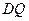 的长度应满足
的长度应满足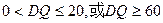 . ………… 10分
. ………… 10分
(注:若通过建立直角坐标系,用解析法参照得分)
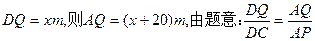 ,
,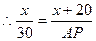 ,
,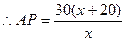 ………… 2分
………… 2分则
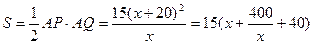
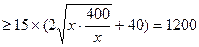 ………… 4分
………… 4分当且仅当
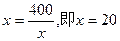 时等号成立………… 5分
时等号成立………… 5分(Ⅱ)由
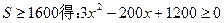 ………… 7分
………… 7分解得:
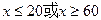
又
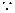
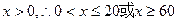 ………… 9分
………… 9分答:(1)
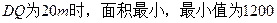 ;
;(2)
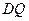 的长度应满足
的长度应满足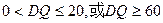 . ………… 10分
. ………… 10分(注:若通过建立直角坐标系,用解析法参照得分)

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
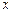 的实系数一元二次方程
的实系数一元二次方程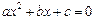 有两个虚数根
有两个虚数根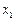 、
、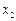 ,若
,若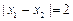 ,且
,且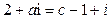 ,求方程的根
,求方程的根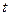 (万元)的关系满足公式P=
(万元)的关系满足公式P=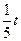 ,Q=
,Q=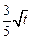 ,现将3万元资金投入经营甲、乙两种商品,设投入乙的资金为x万元,获得的总利润为y(万元)
,现将3万元资金投入经营甲、乙两种商品,设投入乙的资金为x万元,获得的总利润为y(万元)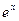 -x-2=0的解在区间(n,n+1)内,n∈N*,根据表格中的数据,则n= ▲ .
-x-2=0的解在区间(n,n+1)内,n∈N*,根据表格中的数据,则n= ▲ .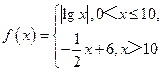 若a,b,c均不相等,且
若a,b,c均不相等,且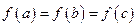 ,则
,则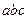 的取值范围是
的取值范围是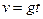 ,则落体从
,则落体从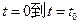 所走过的路程为
所走过的路程为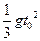
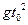
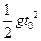
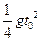
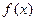 的定义域为
的定义域为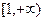 ,且
,且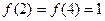 ,
,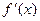 为
为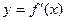 的图象如图所示,则不等式组
的图象如图所示,则不等式组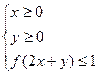 所表示的平面区域的面积是( )
所表示的平面区域的面积是( )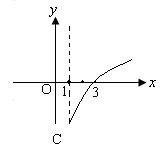
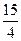
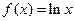 ,
, 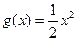 ,
, 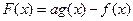 ,
,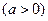 ,若函数
,若函数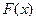 没有零点,求
没有零点,求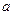 的取值范围;(Ⅱ)若总有
的取值范围;(Ⅱ)若总有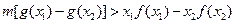 成立,求实数
成立,求实数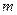 的取值范围.
的取值范围.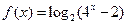 ,则方程
,则方程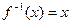 的解为 .
的解为 .