题目内容
6．已知圆C的方程为x2+y2-2x-4y-1=0，直线l：ax+by-4=0（a＞0，b＞0），且直线l始终平分圆C，则ab的最大值为（ ）| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
分析 由题意可得直线经过圆的圆心（1，2），a+2b=4，再利用基本不等式求得ab的最大值．
解答 解：∵直线l：ax+by-4=0（a＞0，b＞0）始终平分圆x2+y2-2x-4y-1=0，
∴直线经过圆的圆心（1，2），
则有a+2b-4=0，即a+2b=4，
由基本不等式可得，a+2b=4≥2$\sqrt{2ab}$，
当且仅当a=2b=2时，取等号，由此可得ab≤2，
∴ab的最大值是2，
故选：B．
点评 本题主要考查了直线和圆相交的性质，基本不等式的应用，解题的关键是直线平分圆的性质的应用，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
17．设F1，F2分别是双曲线3x2-y2=9的左右焦点，若P在双曲线上且$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}=0$，则$|{\overrightarrow{P{F_1}}+\overrightarrow{P{F_2}}}|$的值为 （ ）
| A． | $2\sqrt{5}$ | B． | $2\sqrt{3}$ | C． | $4\sqrt{3}$ | D． | $4\sqrt{5}$ |
14．从一副不含大、小王的52张扑克牌中任意抽出5张，则至少有3张是A的概率为（ ）
| A． | $\frac{{{C}_{4}^{3}C}_{48}^{2}}{{C}_{52}^{5}}$ | B． | $\frac{{{C}_{48}^{3}C}_{4}^{2}}{{C}_{52}^{5}}$ | ||
| C． | 1-$\frac{{{C}_{48}^{1}C}_{4}^{4}}{{C}_{52}^{5}}$ | D． | $\frac{{{C}_{4}^{3}C}_{48}^{2}{{+C}_{4}^{4}C}_{48}^{1}}{{C}_{52}^{5}}$ |
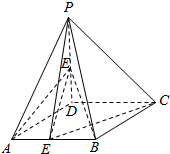如图所示，已知正四棱锥P-ABCD的所有棱长都为1，且E、F分别为AB，PD的中点．