题目内容
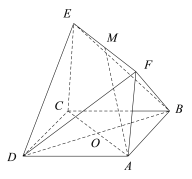
【题目】如图，在四棱锥
中，平面
平面
； 
， 
， 
， 
.
（1）证明： 
平面
；
（2）求直线
与平面
所成的角的正切值.
【答案】（1）详见解析；（2）
.
【解析】试题分析：（1）连结
，在直角梯形
中，由勾股定理证明
，再证平面
平面，从而
平面；（2）在直角梯形中，证明
，再证
平面
.
作
于
的延长线交于
，连结
，证明
平面，从而可得
是直线
与平面所成的角.在
中，求
，在
中，求，在
中，求
，
即得直线与平面所成的角的正切值.
（1）连结，在直角梯形中，由
，
得
，
由
得
，即，
又平面平面，从而平面.
（2）在直角梯形中，由，
得，
又平面平面，所以平面.
作于的延长线交于，连结，则平面，
所以是直线与平面所成的角.
在中，由
，
，得
，
，
在中，
，
，得
，
在中，由，得
，
所以直线与平面所成的角的正切值是.
练习册系列答案
相关题目
【题目】为了了解初三学生女生身高情况，某中学对初三女生身高进行了一次测量，所得数据整理后列出了频率分布表如下：
组 别 | 频数 | 频率 |
[145.5，149.5） | 1 | 0.02 |
[149.5，153.5） | 4 | 0.08 |
[153.5，157.5） | 20 | 0.40 |
[157.5，161.5） | 15 | 0.30 |
[161.5，165.5） | 8 | 0.16 |
[165.5，169.5） | m | n |
合 计 | M | N |
（1）求出表中
所表示的数；
（2）画出频率分布直方图；
