题目内容
7.已知函数f(x)=x3-12x,x∈[-3,3];(1)求f′(x);
(2)求f(x)的最大值与最小值.
分析 (1)根据导数的运算法则求导即可;
(2)根据导数和函数的最值关系,即可求出.
解答 解.(1)f'(x)=3x2-12,x∈[-3,3],
(2)令f'(x)=0,解得x=2,或x=-2(4分)
下面分两种情况讨论:
当f'(x)>0,即:3>x>2,或-3<x<-2时,
当f'(x)<0,即:-2<x<2时,
当x变化时,f'(x),f(x)的变化情款如下表:
| x | -3 | (-3,-2) | -2 | (-2,2) | 2 | (2,3) | 3 |
| f'(x) | + | + | 0 | - | 0 | + | + |
| f(x) | 9 | 单调递增 | 16 | 单调递增 | -16 | 单调递增 | -9 |
点评 本题考查了导数和函数的最值的关系,关键是判断函数的单调区间,属于中档题.

练习册系列答案
相关题目
1.积分$\int_0^4xdx$的值为( )
| A. | 4 | B. | 6 | C. | 8 | D. | 12 |
2.现有5名同学去听同时进行的3个课外知识讲座,每名同学可自由选择其中的一个讲座,不同选法的种数是( )
| A. | C${\;}_{5}^{2}$ | B. | A${\;}_{5}^{2}$ | C. | 35 | D. | 52 |
19.已知随机变量ξ:B(10,0.04),随机变量ξ的数学期望E(ξ)=( )
| A. | 0.2 | B. | 0.4 | C. | 2 | D. | 4 |
12.设z1=-2i,z2=i-2,复数Z1和Z2在复平面内对应点分别为A、B,点O为原点,则△AOB的面积为( )
| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | 4 |
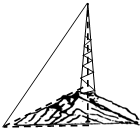 如图,某城市的电视发射塔CD建在市郊的小山上,小山的高BC为30米,在地面上
如图,某城市的电视发射塔CD建在市郊的小山上,小山的高BC为30米,在地面上