题目内容
2.各项均为正整数的数列a1,a2,a3,a4中,前三项依次成公差为d(d>0)的等差数列,后三项依次成公比为q的等比数列,若a4-a1=28,则q的所有可能的值构成的集合为{$\frac{3}{2}$,$\frac{10}{9}$}..分析 由题意设这4个数分别为a1,a1+d,a1+2d,a1+28,其中a1,d均为正整数,由已知条件可得a1和d的关系式,可得d的取值范围,取整数进而可得a1,可得q值
解答 解:由题意设这4个数分别为a1,a1+d,a1+2d,a1+28,其中a1,d均为正整数,
∵后三项依次成公比为q的等比数列
∴(a1+2d)2=(a1+d)(a1+28)
整理得a1=$\frac{4d(7-d)}{3d-28}$>0,
∴(d-7)(3d-28)<0,解得7<d<$\frac{28}{3}$,
则d可能为8,9,
当d=8时,a1=8,q=$\frac{3}{2}$;
当d=9时,a1=72,q=$\frac{10}{9}$;
∴q的所有可能值构成的集合为{$\frac{3}{2}$,$\frac{10}{9}$}.
故答案为:{$\frac{3}{2}$,$\frac{10}{9}$}.
点评 本题考查等差数列和等比数列的综合,涉及分类讨论的思想,属中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.已知O是锐角△ABC的外接圆圆心,∠A=30°,$\frac{cosB}{sinC}$•$\overrightarrow{AB}$+$\frac{cosC}{sinB}$•$\overrightarrow{AC}$=2m•$\overrightarrow{AO}$,则m的值为( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\sqrt{2}$ | C. | 1 | D. | $\frac{1}{2}$ |
14.已知cos(π-α)=-$\frac{3}{5}$,且α是第一象限角,则sin(-2π-α)的值是( )
| A. | $\frac{4}{5}$ | B. | $-\frac{4}{5}$ | C. | ±$\frac{4}{5}$ | D. | $\frac{3}{5}$ |
12.阅读下图所示的程序框图,该框图表示的函数是( )
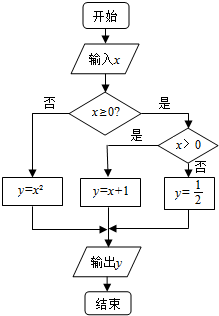

| A. | y=$\left\{\begin{array}{l}{{x}^{2},x≥0}\\{x+1,x<0}\end{array}\right.$ | B. | y=$\left\{\begin{array}{l}{\frac{1}{2},x≥0}\\{{x}^{2},x<0}\end{array}\right.$ | ||
| C. | y=$\left\{\begin{array}{l}{{x}^{2},x<0}\\{\frac{1}{2},x=0}\\{x+1,x>0}\end{array}\right.$ | D. | y=$\left\{\begin{array}{l}{{x}^{2},x>0}\\{\frac{1}{2},x=0}\\{x+1,x<0}\end{array}\right.$ |
 如图是某学校抽取的n个学生体重的频率分布直方图,已知图中从左到右的前3个小组的频率之比为1:2:3,第3小组的频数为18,则n的值是48.
如图是某学校抽取的n个学生体重的频率分布直方图,已知图中从左到右的前3个小组的频率之比为1:2:3,第3小组的频数为18,则n的值是48.