题目内容
已知a,b,c为正数,关于x的一元二次方程ax2+bx+c=0有两个相等的实数根.则方程(a+1)x2+(b+2)x+c+1=0的实数根的个数是( )A.0或1
B.1或2
C.0或2
D.不确定
【答案】分析:先根据关于x的一元二次方程ax2+bx+c=0有两个相等的实根确定出△=b2-4ac=0,再求方程(a+1)x2+(b+2)x+c+1=0的根的判别式,并将△=b2-4ac=0代入其中进行化简,然后根据它与0的大小来判断该方程的根的情况.
解答:解:∵关于x的一元二次方程ax2+bx+c=0有两个相等的实根,
∴△=b2-4ac=0,ac=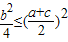
即a+c≥b 或a+c≤-b(舍)
则方程(a+1)x2+(b+2)x+c+1=0的根的判别式为:
△=(b+2)2-4(a+1)(c+1)=b2+4b-4ac-4a-4c=4b-4(a+c)=4b-4(a+c)=4[b-(a+c)]≤0,
∴方程(a+1)x2+(b+2)x+c+1=0的根的个数为0或1个;
故选A.
点评:本题考查了一元二次方程的根的判别式.一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.
解答:解:∵关于x的一元二次方程ax2+bx+c=0有两个相等的实根,
∴△=b2-4ac=0,ac=
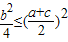
即a+c≥b 或a+c≤-b(舍)
则方程(a+1)x2+(b+2)x+c+1=0的根的判别式为:
△=(b+2)2-4(a+1)(c+1)=b2+4b-4ac-4a-4c=4b-4(a+c)=4b-4(a+c)=4[b-(a+c)]≤0,
∴方程(a+1)x2+(b+2)x+c+1=0的根的个数为0或1个;
故选A.
点评:本题考查了一元二次方程的根的判别式.一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案
相关题目
已知a,b,c为正数,关于x的一元二次方程ax2+bx+c=0有两个相等的实数根.则方程(a+1)x2+(b+2)x+c+1=0的实数根的个数是( )
| A、0或1 | B、1或2 | C、0或2 | D、不确定 |