题目内容
(2013•徐州模拟)[选修4-5:不等式选讲]
已知a,b,c为正数,且满足acos2θ+bsin2θ<c,求证:
cos2θ+
sin2θ<
.
已知a,b,c为正数,且满足acos2θ+bsin2θ<c,求证:
| a |
| b |
| c |
分析:由柯西不等式定理构造不等式
cos2θ+
sin2θ≤[(
cosθ)2+(
sinθ)2]
(cos2θ+sin2θ)
直接证明即可.
| a |
| b |
| a |
| b |
| 1 |
| 2 |
| 1 |
| 2 |
解答:证明:由柯西不等式,得
cos2θ+
sin2θ
≤[(
cosθ)2+(
sinθ)2]
(cos2θ+sin2θ)
=(acos2θ+bsin2θ)
<
.…(10分)
| a |
| b |
≤[(
| a |
| b |
| 1 |
| 2 |
| 1 |
| 2 |
=(acos2θ+bsin2θ)
| 1 |
| 2 |
<
| c |
点评:本题考查了柯西不等式证明不等式的方法,属于基础题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
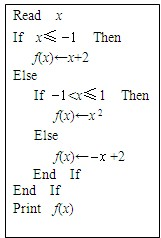 (2013•徐州模拟)已知某算法的伪代码如图,根据伪代码,若函数g(x)=f(x)-m在R上有且只有两个零点,则实数m的取值范围是
(2013•徐州模拟)已知某算法的伪代码如图,根据伪代码,若函数g(x)=f(x)-m在R上有且只有两个零点,则实数m的取值范围是