题目内容
【题目】已知椭圆C: ![]() (a>0,b>0)的离心率为
(a>0,b>0)的离心率为 ![]() ,点A(0,﹣2)与椭圆右焦点F的连线的斜率为
,点A(0,﹣2)与椭圆右焦点F的连线的斜率为 ![]() .
.
(1)求椭圆C的方程;
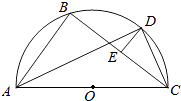
(2)O为坐标原点,过点A的直线l与椭圆C相交于P,Q两点,当△OPQ的面积最大时,求直线l的方程.
【答案】
(1)解:设F(c,0).
∵直线AF的斜率为 ![]() ,
,
∴ ![]() =
= ![]() ,解得c=
,解得c= ![]() .
.
又离心率为e= ![]() =
= ![]() ,
,
由b2=a2﹣c2,解得:a=2,b=1,
∴椭圆E的方程为 ![]() +y2=1.
+y2=1.
(2)解:设P(x1,y1),Q(x2,y2),由题意可设直线l的方程为:y=kx﹣2,与椭圆方程联立,
整理得:(1+4k2)x2﹣16kx+12=0,当△=16(4k2﹣3)>0时,即k2> ![]() 时,
时,
x1+x2= ![]() ,x1x2=
,x1x2= ![]() ,
,
∴|PQ|= ![]() ,
,
∵点O到直线l的距离d= ![]() ,
,
∴S△OPQ= ![]() d|PQ|=
d|PQ|= ![]() ,
,
设 ![]() =t>0,则4k2=t2+3,
=t>0,则4k2=t2+3,
∴S△OPQ= ![]() =
= ![]() ≤1,
≤1,
当且仅当t=2,即 ![]() =2,解得k=±
=2,解得k=± ![]() 时取等号,且满足△>0,
时取等号,且满足△>0,
∴△OPQ的面积最大时,直线l的方程为:y=± ![]() x﹣2
x﹣2
【解析】(1)设F(c,0),利用直线的斜率公式可得关于c的方程,求出c,由离心率e= ![]() =
= ![]() ,求得a,由b2=a2﹣c2 , 求得b的值,即可求得椭圆C的方程;(2)设P(x1 , y1),Q(x2 , y2),由题意可设直线l的方程为:y=kx﹣2,与椭圆的方程联立可得(1+4k2)x2﹣16kx12=0,求出方程的根,从而表示出|PQ|以及点O到直线PQ的距离,从而表示出S△OPQ , 再利用基本不等式的性质即可得出直线l的方程.
,求得a,由b2=a2﹣c2 , 求得b的值,即可求得椭圆C的方程;(2)设P(x1 , y1),Q(x2 , y2),由题意可设直线l的方程为:y=kx﹣2,与椭圆的方程联立可得(1+4k2)x2﹣16kx12=0,求出方程的根,从而表示出|PQ|以及点O到直线PQ的距离,从而表示出S△OPQ , 再利用基本不等式的性质即可得出直线l的方程.

【题目】![]() 市某机构为了调查该市市民对我国申办
市某机构为了调查该市市民对我国申办![]() 年足球世界杯的态度,随机选取了
年足球世界杯的态度,随机选取了![]() 位市民进行调查,调查结果统计如下:
位市民进行调查,调查结果统计如下:
支持 | 不支持 | 合计 | |
男性市民 |
| ||
女性市民 |
| ||
合计 |
|
|
(1)根据已知数据,把表格数据填写完整;
(2)利用(1)完成的表格数据回答下列问题:
(i)能否在犯错误的概率不超过![]() 的前提下认为支持申办足球世界杯与性别有关;
的前提下认为支持申办足球世界杯与性别有关;
(ii)已知在被调查的支持申办足球世界杯的男性市民中有![]() 位退休老人,其中
位退休老人,其中![]() 位是教师,现从这
位是教师,现从这![]() 位退休老人中随机抽取
位退休老人中随机抽取![]() 人,求至多有
人,求至多有![]() 位老师的概率.
位老师的概率.
附:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|