题目内容
【题目】如图所示,AC为⊙O的直径,D为 ![]() 的中点,E为BC的中点.
的中点,E为BC的中点. 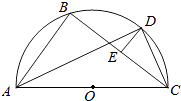
(1)求证:DE∥AB;
(2)求证:ACBC=2ADCD.
【答案】
(1)证明:连接BD,

因为D为 ![]() 的中点,所以BD=DC.
的中点,所以BD=DC.
因为E为BC的中点,所以DE⊥BC.
因为AC为圆的直径,所以∠ABC=90°,
所以AB∥DE.…(5分)
(2)证明:因为D为 ![]() 的中点,所以∠BAD=∠DAC,
的中点,所以∠BAD=∠DAC,
又∠BAD=∠DCB,则∠DAC=∠DCB.
又因为AD⊥DC,DE⊥CE,所以△DAC∽△ECD.
所以 ![]() =
= ![]() ,ADCD=ACCE,2ADCD=AC2CE,
,ADCD=ACCE,2ADCD=AC2CE,
因此2ADCD=ACBC.
【解析】(1)欲证DE∥AB,连接BD,因为D为 ![]() 的中点及E为BC的中点,可得DE⊥BC,因为AC为圆的直径,所以∠ABC=90°,最后根据垂直于同一条直线的两直线平行即可证得结论;(2)欲证ACBC=2ADCD,转化为ADCD=ACCE,再转化成比例式
的中点及E为BC的中点,可得DE⊥BC,因为AC为圆的直径,所以∠ABC=90°,最后根据垂直于同一条直线的两直线平行即可证得结论;(2)欲证ACBC=2ADCD,转化为ADCD=ACCE,再转化成比例式 ![]() =
= ![]() .最后只须证明△DAC∽△ECD即可.
.最后只须证明△DAC∽△ECD即可.

练习册系列答案
相关题目
【题目】为调查某地区老人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
性别 是否需要志愿者 | 男 | 女 |
需要 | 40 | 30 |
不需要 | 160 | 270 |
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)请根据上面的数据分析该地区的老年人需要志愿者提供帮助与性别有关吗

