题目内容
已知:正四棱柱ABCD—A1B1C1D1中,底面边长为2 ,侧棱长为4,E、F分别为棱AB、BC的中点.
,侧棱长为4,E、F分别为棱AB、BC的中点.
(1)求证:平面B1EF⊥平面BDD1B1;
(2)求点D1到平面B1EF的距离.
 ,侧棱长为4,E、F分别为棱AB、BC的中点.
,侧棱长为4,E、F分别为棱AB、BC的中点.(1)求证:平面B1EF⊥平面BDD1B1;
(2)求点D1到平面B1EF的距离.
(1)证明略 (2)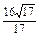
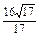
(1) 建立如图所示的空间直角坐标系,则D(0,0,0),
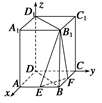
B(2 ,2
,2 ,0),E(2
,0),E(2 ,
, ,0),
,0),
F( ,2
,2 ,0),D1(0,0,4),
,0),D1(0,0,4),
B1(2 ,2
,2 ,4).
,4).
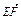 =(-
=(- ,
, ,0),
,0),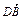 =(2
=(2 ,2
,2 ,0),
,0),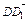 =(0,0,4),
=(0,0,4),
∴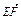 ·
·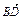 =0,
=0,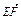 ·
·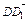 =0.
=0.
∴EF⊥DB,EF⊥DD1,DD1∩BD=D,
∴EF⊥平面BDD1B1.
又EF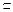 平面B1EF,∴平面B1EF⊥平面BDD1B1.
平面B1EF,∴平面B1EF⊥平面BDD1B1.
(2) 由(1)知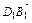 =(2
=(2 ,2
,2 ,0),
,0),
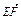 =(-
=(- ,
, ,0),
,0),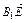 =(0,-
=(0,- ,-4).
,-4).
设平面B1EF的法向量为n,且n=(x,y,z)
则n⊥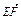 ,n⊥
,n⊥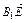
即n·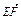 =(x,y,z)·(-
=(x,y,z)·(- ,
, ,0)=-
,0)=- x+
x+ y=0,
y=0,
n·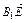 =(x,y,z)·(0,-
=(x,y,z)·(0,- ,-4)=-
,-4)=- y-4z=0,
y-4z=0,
令x=1,则y=1,z=-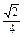 ,∴n="(1,1,-"
,∴n="(1,1,-" 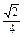 )
)
∴D1到平面B1EF的距离
d=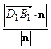 =
=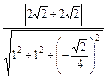 =
=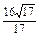 .
.

B(2
 ,2
,2 ,0),E(2
,0),E(2 ,
, ,0),
,0),F(
 ,2
,2 ,0),D1(0,0,4),
,0),D1(0,0,4),B1(2
 ,2
,2 ,4).
,4).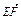 =(-
=(- ,
, ,0),
,0),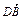 =(2
=(2 ,2
,2 ,0),
,0),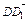 =(0,0,4),
=(0,0,4),∴
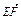 ·
·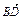 =0,
=0,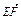 ·
·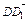 =0.
=0.∴EF⊥DB,EF⊥DD1,DD1∩BD=D,
∴EF⊥平面BDD1B1.
又EF
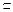 平面B1EF,∴平面B1EF⊥平面BDD1B1.
平面B1EF,∴平面B1EF⊥平面BDD1B1.(2) 由(1)知
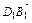 =(2
=(2 ,2
,2 ,0),
,0),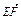 =(-
=(- ,
, ,0),
,0),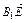 =(0,-
=(0,- ,-4).
,-4).设平面B1EF的法向量为n,且n=(x,y,z)
则n⊥
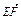 ,n⊥
,n⊥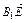
即n·
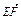 =(x,y,z)·(-
=(x,y,z)·(- ,
, ,0)=-
,0)=- x+
x+ y=0,
y=0,n·
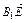 =(x,y,z)·(0,-
=(x,y,z)·(0,- ,-4)=-
,-4)=- y-4z=0,
y-4z=0,令x=1,则y=1,z=-
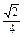 ,∴n="(1,1,-"
,∴n="(1,1,-" 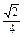 )
)∴D1到平面B1EF的距离
d=
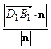 =
=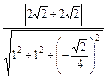 =
=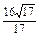 .
.
练习册系列答案
相关题目
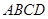 中,
中,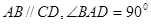 ,
,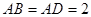 ,
,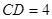 ,点
,点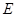 为线段
为线段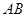 上异于
上异于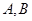 的点,且
的点,且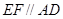 ,沿
,沿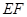 将面
将面 折起,使平面
折起,使平面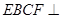 平面
平面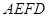 ,如图2.
,如图2.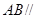 平面
平面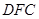 ;
;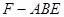 体积最大时,求平面
体积最大时,求平面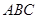 与平面
与平面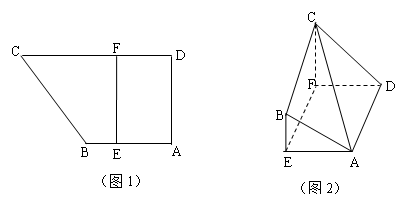
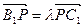 ,当 B1D⊥面PMN时,求
,当 B1D⊥面PMN时,求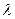 的值.
的值.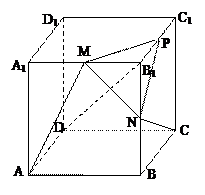
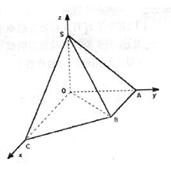
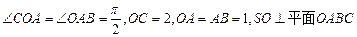 ,SO=1,以OC、OA、OS分别为x轴、y轴、z轴建立直角坐标系O-xyz.
,SO=1,以OC、OA、OS分别为x轴、y轴、z轴建立直角坐标系O-xyz.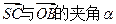 的大小(用反三角函数表示);
的大小(用反三角函数表示);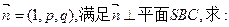
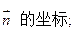
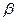 (用反三角函数表示);
(用反三角函数表示);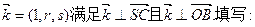
 .
. 
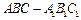 中,底面是等腰直角三角形,
中,底面是等腰直角三角形,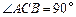 ,侧棱
,侧棱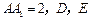 分别是
分别是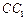 与
与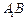 的中点,点
的中点,点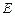 在平面
在平面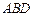 上的射影是
上的射影是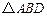 的重心
的重心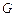 ,求点
,求点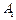 到平面
到平面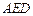 的距离.
的距离.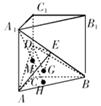
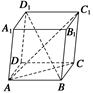
 类比此性质,如下图,在四面体P-ABC中,若PA、PB、PC两两垂直,底面ABC上的高为h,则得到的正确结论为__________________________.
类比此性质,如下图,在四面体P-ABC中,若PA、PB、PC两两垂直,底面ABC上的高为h,则得到的正确结论为__________________________.
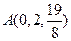 ,
,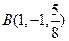 ,
,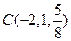 是平面
是平面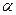 内的三点,设平面
内的三点,设平面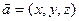 ,则
,则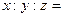 ________________。
________________。