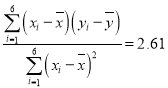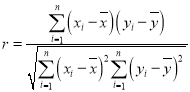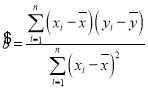题目内容
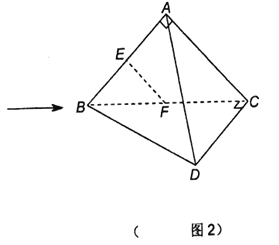
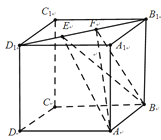
【题目】如图，正方体ABCD﹣A1B1C1D1的棱长为1，线段B1D1上有两个动点E、F，且EF=
．则下列结论中正确的个数为
①AC⊥BE；
②EF∥平面ABCD；
③三棱锥A﹣BEF的体积为定值；
④
的面积与
的面积相等，
A.4B.3C.2D.1
【答案】B
【解析】
试题①中AC⊥BE，由题意及图形知，AC⊥面DD1B1B，故可得出AC⊥BE，此命题正确；②EF∥平面ABCD，由正方体ABCD-A1B1C1D1的两个底面平行，EF在其一面上，故EF与平面ABCD无公共点，故有EF∥平面ABCD，此命题正确；③三棱锥A-BEF的体积为定值，由几何体的性质及图形知，三角形BEF的面积是定值，A点到面DD1B1B距离是定值，故可得三棱锥A-BEF的体积为定值，此命题正确；④由图形可以看出，B到线段EF的距离与A到EF的距离不相等，故△AEF的面积与△BEF的面积相等不正确
练习册系列答案
相关题目
