题目内容
在平行四边形ABCD中,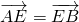 ,
,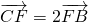 ,连接CE、DF相交于点M,若
,连接CE、DF相交于点M,若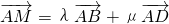 ,则实数λ与μ的乘积为
,则实数λ与μ的乘积为
- A.

- B.

- C.

- D.

B
分析:由题意可得 =2(λ-μ)
=2(λ-μ) +μ
+μ ,由E、M、C三点共线,可得2λ-μ=1,①同理可得
,由E、M、C三点共线,可得2λ-μ=1,①同理可得 =
=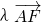
 ,由D、M、F三点共线,可得
,由D、M、F三点共线,可得 λ+μ=1,②,综合①②可得数值,作乘积即可.
λ+μ=1,②,综合①②可得数值,作乘积即可.
解答:由题意可知:E为AB的中点,F为BC的三等分点(靠近B)
故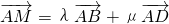 =
=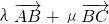 =
=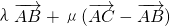
=(λ-μ) +μ
+μ =2(λ-μ)
=2(λ-μ) +μ
+μ ,
,
因为E、M、C三点共线,故有2(λ-μ)+μ=1,即2λ-μ=1,①
同理可得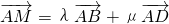 =
=
=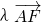

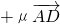 =
=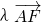
 ,
,
因为D、M、F三点共线,故有λ+(μ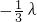 )=1,即
)=1,即 λ+μ=1,②
λ+μ=1,②
综合①②可解得λ= ,
,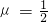 ,故实数λ与μ的乘积
,故实数λ与μ的乘积 =
=
故选B
点评:本题考查平面向量基本定理即意义,涉及三点共线的结论,属中档题.
分析:由题意可得
 =2(λ-μ)
=2(λ-μ) +μ
+μ ,由E、M、C三点共线,可得2λ-μ=1,①同理可得
,由E、M、C三点共线,可得2λ-μ=1,①同理可得 =
=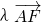
 ,由D、M、F三点共线,可得
,由D、M、F三点共线,可得 λ+μ=1,②,综合①②可得数值,作乘积即可.
λ+μ=1,②,综合①②可得数值,作乘积即可.解答:由题意可知:E为AB的中点,F为BC的三等分点(靠近B)
故
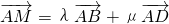 =
=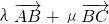 =
=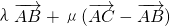
=(λ-μ)
 +μ
+μ =2(λ-μ)
=2(λ-μ) +μ
+μ ,
,因为E、M、C三点共线,故有2(λ-μ)+μ=1,即2λ-μ=1,①
同理可得
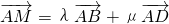 =
=
=
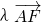

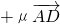 =
=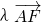
 ,
,因为D、M、F三点共线,故有λ+(μ
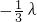 )=1,即
)=1,即 λ+μ=1,②
λ+μ=1,②综合①②可解得λ=
 ,
,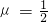 ,故实数λ与μ的乘积
,故实数λ与μ的乘积 =
=
故选B
点评:本题考查平面向量基本定理即意义,涉及三点共线的结论,属中档题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 如图,在平行四边形ABCD中,边AB所在直线方程为2x-y-3=0,点C(3,0).
如图,在平行四边形ABCD中,边AB所在直线方程为2x-y-3=0,点C(3,0).