题目内容
 如图,在平行四边形ABCD中,边AB所在直线方程为2x-y-3=0,点C(3,0).
如图,在平行四边形ABCD中,边AB所在直线方程为2x-y-3=0,点C(3,0).(1)求直线CD的方程;
(2)求AB边上的高CE所在直线的方程.
分析:(1)根据两直线平行的性质,求出直线的斜率,用点斜式求出直线方程,并化为一般式.
(2)根据两直线垂直的性质,求出直线的斜率,用点斜式求出直线方程,并化为一般式.
(2)根据两直线垂直的性质,求出直线的斜率,用点斜式求出直线方程,并化为一般式.
解答: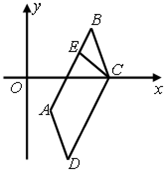 解:(1)由题意知,CD∥AB,KCD=KAB=2,
解:(1)由题意知,CD∥AB,KCD=KAB=2,
由点斜式求出直线CD的方程为y=2(x-3),即2x-y-6=0.
(2)由题意知,CE⊥AB,KCE•KAB=-1,∴KCE=-
.
∴AB边上的高CE所在直线的方程为 y=-
(x-3),即x+2y-3=0.
 解:(1)由题意知,CD∥AB,KCD=KAB=2,
解:(1)由题意知,CD∥AB,KCD=KAB=2,由点斜式求出直线CD的方程为y=2(x-3),即2x-y-6=0.
(2)由题意知,CE⊥AB,KCE•KAB=-1,∴KCE=-
| 1 |
| 2 |
∴AB边上的高CE所在直线的方程为 y=-
| 1 |
| 2 |
点评:本题主要考查两直线平行和垂直的性质,用点斜式求直线方程,属于基础题.

练习册系列答案
相关题目
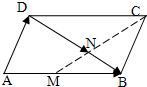
 如图,在平行四边形ABCD中,下列结论中错误的是( )
如图,在平行四边形ABCD中,下列结论中错误的是( )A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
 如图,在平行四边形ABCD,
如图,在平行四边形ABCD, 如图,在平行四边形ABCD中,
如图,在平行四边形ABCD中,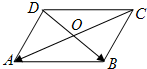 如图,在平行四边形ABCD中,若
如图,在平行四边形ABCD中,若 如图,在平行四边形OABC中,点O是原点,点A和点C的坐标分别是(3,0)、(1,3),点D是线段AB上的中点.
如图,在平行四边形OABC中,点O是原点,点A和点C的坐标分别是(3,0)、(1,3),点D是线段AB上的中点.